Measure-Valued Derivatives for Reinforcement Learning
Introduction
Reinforcement learning methods for robotics are increasingly successful due to the constant development of better policy gradient techniques. A precise (low variance) and accurate (low bias) gradient estimator is crucial to face increasingly complex tasks. Traditional policy gradient algorithms use the likelihood-ratio trick (or score function), which is known to produce unbiased but high variance estimates. More modern approaches exploit the reparametrization trick (RepTrick), which gives lower variance gradient estimates but requires differentiable value function approximators. In this work, we study a different type of stochastic gradient estimator: the Measure-Valued Derivative (MVD).
Methods
Our research consisted in empirically comparing the performance of stochastic gradient estimators in high-dimensional continuous control tasks in robotics simulators. The idea behind these estimators is to compute the gradient of an expectation (the sum of rewards in a reinforcement learning task) with respect to distributional parameters. This computation is not easy, because the gradient of an expectation does not necessarily results in an expectation that can be solved through sampling. There are three known techniques to produce unbiased samples of the stochastic gradient – score-function, reparametrization trick and measure-valued derivative. In this work we studied these estimators in the context of policy optimization in reinforcement learning. We start from deriving the policy gradient using the different stochastic gradient estimators, and compare their errors in magnitude and direction with respect to the true gradient. Afterwards we empirically evaluate the estimators in different environments in on- and off-policy settings in increasingly more difficult tasks, from the Linear Quadratic Regulator to the MuJoCo simulator robotic tasks.
Results
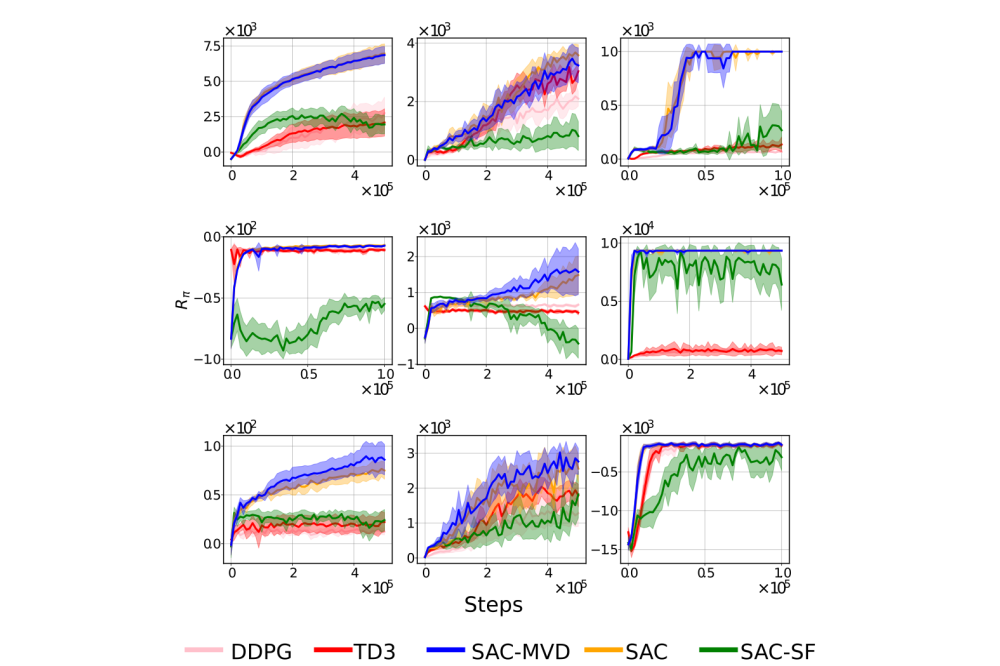
Our results showed two important aspects. The measure-valued derivative estimator has less variance that then score-function, and that we can replace the reparametrization trick with the measure-valued derivative in the soft-actor critic algorithm, a state-of-the-art off-policy gradient method. The results are in line with the theory, and are a proof of concept that the measure-valued derivative estimator can be used as a replacement of the other estimators. In the linear quadratic regulator experiment, because we have access to the true gradient estimate, we can exactly compute the absolute error both in magnitude and in direction via the cosine distance. Our experiments showed that the errors from the measure-valued derivative estimator are between the score-function and reparametrization trick. Additionally, this aspect translates to faster learning measured by the steps to achieve a higher return. In the off-policy experiments, we observed that in the soft-actor critic algorithm we can replace the reparametrization trick with the measurevalued derivative without any loss of performance. This fact allows us to replace neural networks that approximate the state-action value function with non-differentiable function approximators, such as regression trees.
Discussion
In this work we present measure-valued derivatives as a complement to the score-function and reparametrization trick estimators for actor-critic policy gradient algorithms. We empirically show that methods based on this estimator are a viable alternative to the commonly used ones, and most importantly we avoid resetting the system to a specific state as done in previous works, which is impractical in real systems, showing how MVDs are applicable to the general reinforcement learning framework.