Distributionally Robust Trajectory Optimization Under Uncertain Dynamics via Relative-Entropy Trust Regions
Belousov, Boris_Sample-efficient and robust Bayesian robot learningFigure 1: Comparison of standard (blue/green) and distributionally robust (red/magenta) controllers on a mass-spring-damper linear system evaluated on the nominal dynamics (left) and under the worst-case disturbance (middle). Trust-region KL-divergence (KLD) budget over time in the worst-case setting (top right) and expected cost as a function of the disturbance (bottom right) illustrate the performance of the proposed method.
Boris Belousov
Introduction
Trajectory optimization and model predictive control are essential techniques underpinning advanced robotic applications, ranging from autonomous driving to full-body humanoid control. State-of-the-art algorithms have focused on data-driven approaches that infer the system dynamics online and incorporate posterior uncertainty during planning and control. Despite their success, such approaches are still susceptible to catastrophic errors that may arise due to statistical learning biases, unmodeled disturbances or even directed adversarial attacks. In this project, we tackle the problem of dynamics mismatch and propose a distributionally robust optimal control formulation that alternates between two relative entropy trust region optimization problems. Our method finds the worst-case maximum entropy Gaussian posterior over the dynamics parameters and the corresponding robust optimal policy. We show that our approach admits a closed-form backward-pass for a certain class of systems and demonstrate the resulting robustness on linear and nonlinear problems.
Methods
Our approach brings together several strands of research. First, we rely on distributionally robust optimization to find the worst-case parameter distribution. Second, our problem formulation is based on an iterative scheme of relative entropy policy search, a trust region algorithm for policy optimization. Third, we employ iterative linearization and approximate integration to enable applications to nonlinear uncertain dynamical systems. To evaluate the proposed method, we run extensive simulations on the cluster.
Results
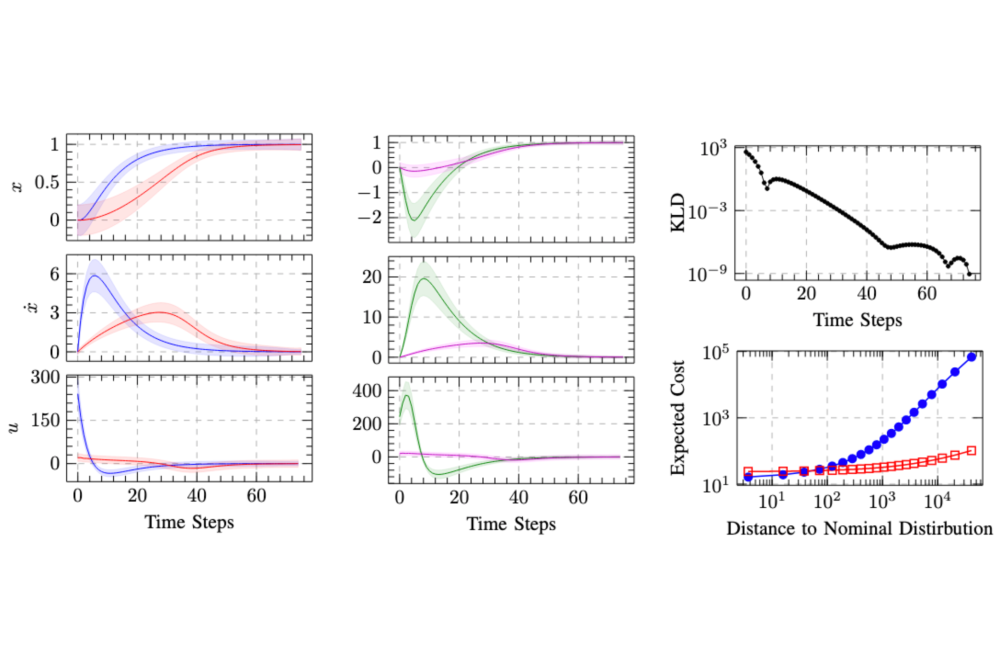
We have presented a technique to robustify data-driven stochastic optimal control approaches that rely on probabilistic models of the dynamics. Our approach consists of an iterative two-stage relative-entropy trust region optimization. The first stage optimizes the maximum entropy worst-case Gaussian distributional dynamics in a KL-ball around a nominal distribution, while the second stage optimizes the policy w.r.t. worst-case dynamics. We have shown that for probabilistic time-variant dynamics models, both stages admit a closed-form backward-pass and a cubature-based forward-pass.
Discussion
We have validated our results on linear and nonlinear dynamical systems and have shown the clear benefit of robustifying standard optimal controllers against worst-case disturbances of learned dynamics. Further research will focus on relaxing the Gaussian assumption of the nominal and worst-case distributions. Moreover, extensions for including online learning of statistical dynamics models and receding horizon control are of interest.
