Policy Optimization with Learning and Planning in Continuous Spaces
Joao Carvalho_Policy Optimization with Learning and Planning in Continuous Spaces_Figure1Figure 1: This figure presents the 3 steps of our VE-PGS algorithm. A) The method starts from the current state s0. B) By running the simulation policy the search tree is temporarily expanded and collects intermediate rewards. C) The rewards obtained during the simulation phase are propagated back to the node s0. These steps are repeated until convergence or a predefined computation budget.
Joao CarvalhoIntroduction
Planning algorithms have shown impressive performance in many domains such as chess and Go. In particular, Monte Carlo Tree Search (MCTS) is used, which builds a search tree toward more promising nodes, while maintaining node statistics to estimate the value of each node. However, these statistics are inaccurate for a small number of visits and the memory requirements for the tree can become unsustainable for large action spaces. A solution to this problem is presented by Policy Gradient Search (PGS). This search method is not based on node statistics but rather learns a simulation policy during the search that guides it toward higher-value nodes. No search tree is needed, which reduces memory requirements. Still, this method suffers from several problems, such as high variance in its value estimates, and is limited to tasks where a perfect simulator of the environment is available. These issues prevent the use of the method in real-world tasks e.g. in logistics or medicine. In this work, we address these problems by proposing a new algorithm: Value Equivalence for Policy Gradient Search (VE-PGS), which uses a modified search of PGS on a value equivalent (VE) model. VE models are learned models that only focus on those parts of the environment that are relevant to the search. Furthermore, we propose several changes to PGS to address its issues, which are then incorporated into VE-PGS.
Methods
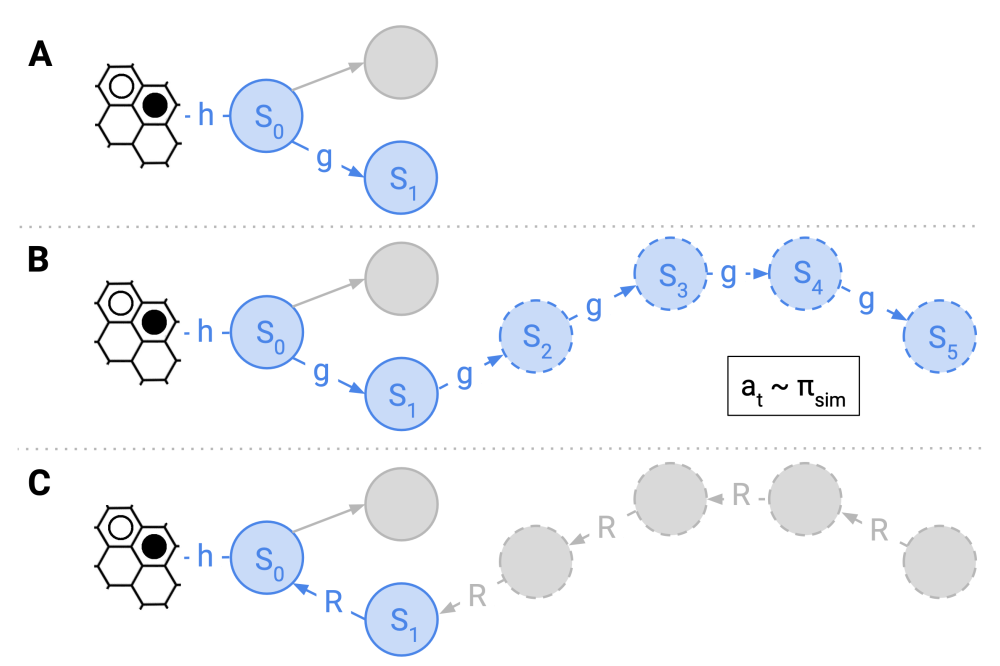
One of the most severe limitations currently hindering the use of Policy Gradient Search (PGS) in real-world problems such as discovering treatment policies in medicine, is the need for a model of the environment. Model-based reinforcement learning (MBRL) provides a solution to this problem by first learning the dynamics of the problem, which can then be used for planning. Typically, the model is learned to match the state transitions encountered during sampling, which makes the model very general and usable for other problems in the same environment. But the capacity of model approximators is limited, so they cannot perfectly represent all aspects of the environment. To use these resources more efficiently, the principle of value equivalence (VE) suggests considering the future use of the model beforehand and focusing on the aspects of the environment that are important for valuebased planning. Driven by the success of MuZero and VE, we present our method of Value Equivalence for Policy Gradient Search (VE-PGS). This approach combines our extended version of PGS with VE models, integrating the simulation policy into the model, so it can make use of a shared state representation. We thus demonstrate the first method based on PGS that does not require knowledge of the dynamics of the environment. Furthermore, using Expert Iteration (Exit), we propose a learning procedure for training a policy with VEPGS tabula rasa, i.e. without prior knowledge of the problem. In addition, we propose extensions to PGS to address the high variance problems and improve performance.
Results
We have shown the effectiveness of the dynamic length, the weighted return and the modified policy target extensions. The other three extensions of the entropy bonus, the KL penalty and the modified update, however, showed little improvement. We attribute this result to the difficulty of learning the simulation policy with few iterations and using only value estimates instead of returns in a sparse reward setting. Nevertheless, these ideas have already been successfully used in other domains. So there are strong indications that these extensions are also useful. By combining these extensions, we were able to show further improvements in comparison to the original version of PGS, especially for a low number of iterations that were smaller than the number of possible actions. In comparison with baseline methods, we could show that PGS can achieve good results and is competitive with AlphaZero. In further experiments, we showed the effectiveness of our method VE-PGS, which operates without knowledge of the dynamics, in comparison with MuZero. Both had equal playing strength when paired together. However, VE-PGS performed better when tested against the extended version of PGS and also won games faster and more accurately than MuZero, thus we concluded that VE-PGS can handle model inaccuracies better and chooses actions more greedily. Since the search tree is not expanded, the memory consumption of our methods is lower and constant, while it grows linearly for MCTS-based methods. Still, performance remains competitive. This feature makes the search suitable for resource-intensive problems e.g. ones with large branching factors.
Discussion
In this work, we have presented the method of Value Equivalence for Policy Gradient Search (VE-PGS), which combines tree-less search with VE models and thus enables planning on environments for which no simulator or knowledge about the dynamic is available. Our approach is based on Policy Gradient Search (PGS), which instead of building a tree structure trains a simulation policy during the search that guides it towards higher valued nodes. The advantages of the method are the generalization capabilities of the simulation policy as well as the significantly reduced memory consumption. Still, there are several limitations, such as the high variance of the sampled trajectories, the lack of exploration and the policy targets, which do not work for small numbers of iterations.
