Hartree-Fock Many-Body Perturbation Theory
Introduction
In modern nuclear structure theory, interactions are constructed from the fundamental symmetries imposed by quantum chromodynamics (QCD). The derived Hamiltonians allow for a realistic description of nuclear observables. Furthermore, the Hamiltonian is evolved by means of the Similarity Renormalization Group (SRG) in order to soften short-range repulsion and tame tensor correlation effects.
Methods
In order to access ground-state energies for medium heavy closed-shell nuclei different frameworks have been considered. An obvious approach is many-body perturbation theory. One starts with defining an additive splitting of a given Hamiltonian and assumes that the exact eigenfunction may be expanded in terms of a power series. By deriving the expansion coefficients we
can deduce the corresponding observables of interest.
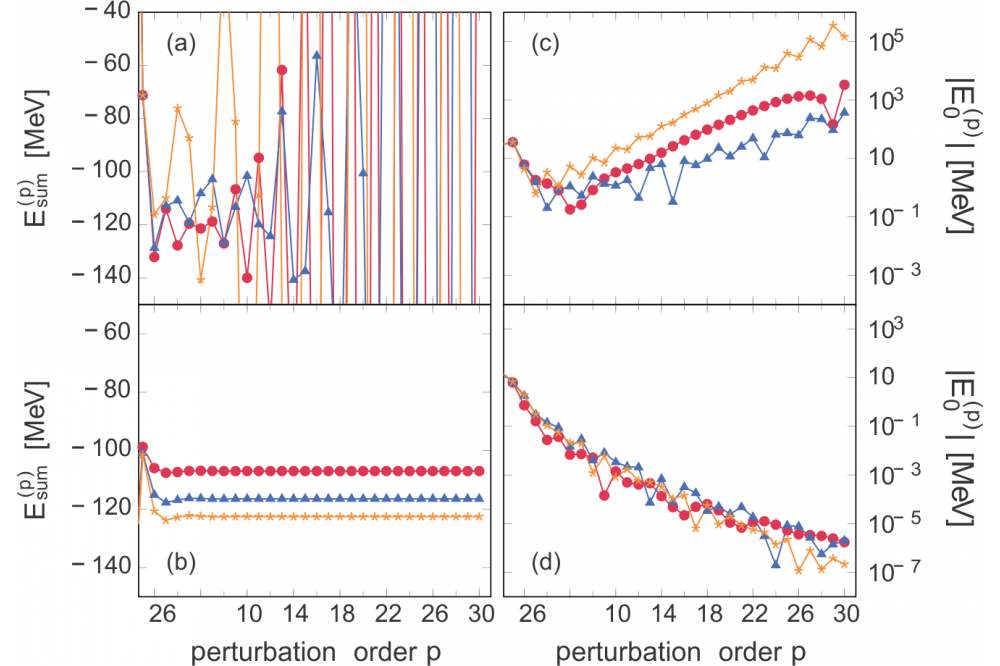
However, perturbation theory requires a convergent power series expansion. We have shown that the choice of the partitioning heavily affects the convergence behaviour of the perturbation series. Prior analysis in terms of harmonic oscillator (HO) single-particle states revealed divergent power series expansions. In recent calculations we were able to overcome this problem by
using Hartree-Fock (HF) single-particle states (Fig. 1).
We started with deriving high-order corrections of the perturbation series by means of a recursive formulation. This enables for a deeper understanding of the perturbative expansion. Moreover, we investigated the impact of the SRG flow parameter on the convergence properties of the perturbation series. It has been shown that perturbation series from Hartree-Fock many-body
perturbation theory (HF-MBPT) are sensitive to the flow parameter. In particular, increasing its value induces a stronger suppression of higher-order corrections. This property is not present in HO-MBPT.
Results
In order to compare the results of HF-MBPT we used the configuration interaction (CI) framework that solves for the ground-state energy by using Lanczos algorithms. Both high-order MBPT and CI calculations require strong use of parallelisation in a hybrid MPI/ OpenMP framework.
Discussion
However, due to computational requirements these approaches are limited to light nuclei. Motivated by the promising results from the high-order MBPT calculations we expect low-order partial sums to be a reasonable approximation for the ground-state energy. Exploiting symmetries of the Hamiltonian enables calculations of ground-state energies up to heavy tin isotopes. The
results were in good agreement to coupled cluster (CC) and in-medium similarity renormalization group (IM-SRG) calculations, which both have shown their reliability in the past.
Outlook
In the future we will extend HF-MBPT to the open-shell region and the calculation of spectra. This requires a treatment of degeneracies by means of a full diagonalization of the subspaces. First calculations for oxygen isotopes showed that high-order HF-MBPT is also robust in the degenerate setting. Formulating low-order energy corrections will allow us to proceed to medium-mass open-shell systems. Furthermore, by deriving low-order state corrections we are able to calculate other nuclear
observables through the corresponding one- and twobody density matrices.
Additionally, we will focus on expanding the closedshell treatment up to fourth order and the derivation of ladder- and ring-type resummations. This allows for the analysis of error bounds intrinsic in the MBPT framework.