Spectral Functions and Transport Coefficients of Matter under Extreme Conditions
Spectral Functions and Transport Coefficients 1Fig. 1: Spectral functions of pion and sigma meson as a function of energy and momentum at a temperature of T=100 MeV.
Introduction
A few milliseconds after the Big Bang, the universe was about 200,000 times hotter than the core of the sun, so that matter existed in the so-called quark-gluon plasma phase with quarks and gluons interacting as described by Quantum Chromodynamics (QCD). Such extreme conditions of matter are nowadays being recreated in heavy ion collision experiments as carried out for example at CERN, the Brookhaven National Laboratory (BNL), or the future Facility for Antiproton and Ion Research (FAIR) where exteremely hot and dense matter will be investigated with the Compressed Baryonic Matter (CBM) experiment.
Methods
In our project, we use effective models of QCD, the theory of strong interactions, to investigate the properties of such hot and dense matter. In particular, our aim is to calculate spectral functions, which contain information on particle masses, life-times, and decay channels as well as transport coefficients like the shear viscosity of hot and dense matter.
Our calculations are based on the Functional Renormalization Group (FRG) as a non-perturbative continuum field theory framework for originally Euclidean correlation functions. The calculation of spectral functions from these Euclidean correlations is normally a numerically ill-posed inverse problem such as an inverse Laplace transform.
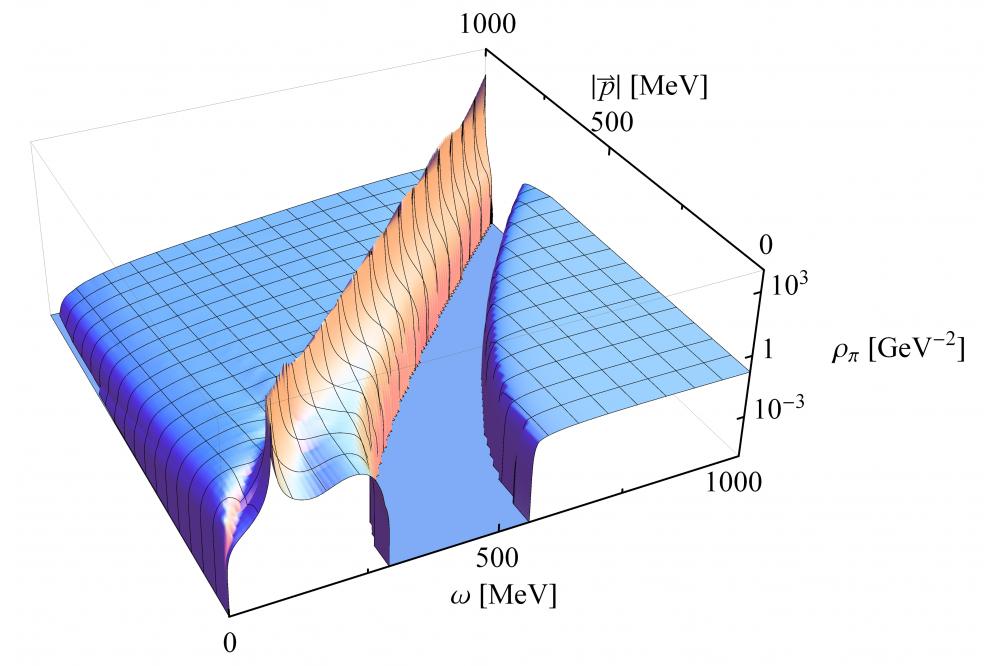
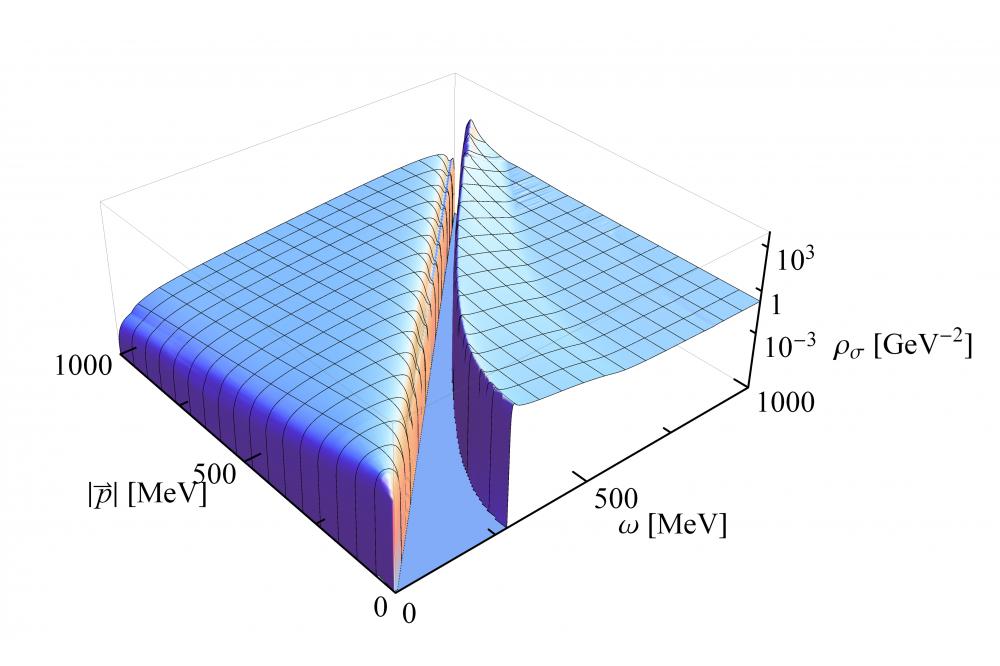
We have developed a new approach based on analytic continuation of the FRG flow equations to avoid this problem.[1,2] With this new method we are now able to calculate the energy and momentum dependence of mesonic spectral functions, cf. Fig. 1, which are needed as input to compute transport coefficients like the shear viscosity of the corresponding hot and dense medium in a next step.
Results
The obtained spectral functions show many interesting features which can be interpreted in terms of different in-medium particle creation and annihilation processes. The sigma spectral function for example, cf. Fig. 1, shows a non-vanishing regime at energies larger than two times the pion mass, where a sigma particle can decay into two pions. At energies smaller then the corresponding spatial momentum we also find non-vanishing values for the spectral function, since here space-like processes like the emission or absorption of a particle can occur. The pion spectral function shows a similar behavior in the space-like regime and for higher energies, where a pion can for example decay into a sigma meson and a pion or into a quark anti-quark pair. At small time-like energies we see that the pion spectral function exhibits a peak that determines its mass and which is Lorentzboosted to higher energies for larger spatial momenta.
Outlook
As an outlook, we aim at further improving our framework, for example by employing the Polyakov quark-meson model which takes important confinement properties into account, and by studying the scale-dependence of wave function renormalization factors which will allow us to also calculate quark spectral functions. Our results were obtained with MPI-code on typically 256 CPU cores in parallel on the Loewe-CSC at Frankfurt University and the Lichtenberg high-performance computer at TU Darmstadt.
