Ultrafast Laser Induced Structural Motion in Thin Au Films
Introduction
Methods
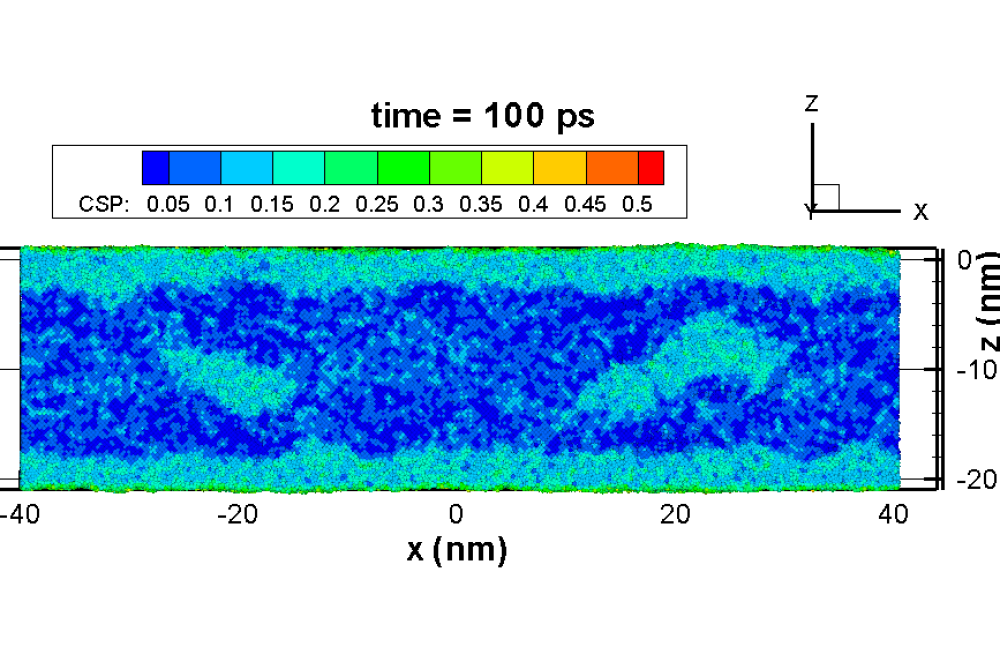
The Molecular-Dynamics Two-Temperature model (MD-TTM) is a combination of the Molecular Dynamics and the TTM simulations, where the two models are interconnected within a unified scheme with feedback, so that each model affects the other. To this end, the MD method completely substitutes the TTM equation for the lattice temperature. The diffusion equation for the electron temperature Te is solved by a finite difference method simultaneously with MD integration of the equations of motion of atoms. A coupling term is responsible for the energy exchange between the electrons and the lattice. Although the MD-TTM model is able to simulate large scale samples in a reasonable amount of time, it was not possible to model the entire sample that was used in the experiment. We thus limit the simulated area to the edge of the laser pulse, where the fluence is high enough to induce melting but not enough to reach the ablation or evaporation threshold. The simulations presented here are performed for free-standing thin Au film with an fcc crystal structure in the (100) orientation, where free boundary conditions were applied at both the top and bottom surfaces of the film. Periodic boundary conditions are imposed in the directions parallel to the free surfaces. These conditions simulate the situation in which the laser spot diameter is large compared to the depth of the laser energy deposition so that an homogeneous energy distribution is considered for the electrons. The reference monocrystalline structure is generated with a total of 11669056 atoms with a volume of 100x100x20 nm. Other thicknesses were used during our study, ranging from 8 nm to 33 nm. Hundreds of simulations have been performed since the begining of this project which could only have been done with a lot of computational ressources.
Results
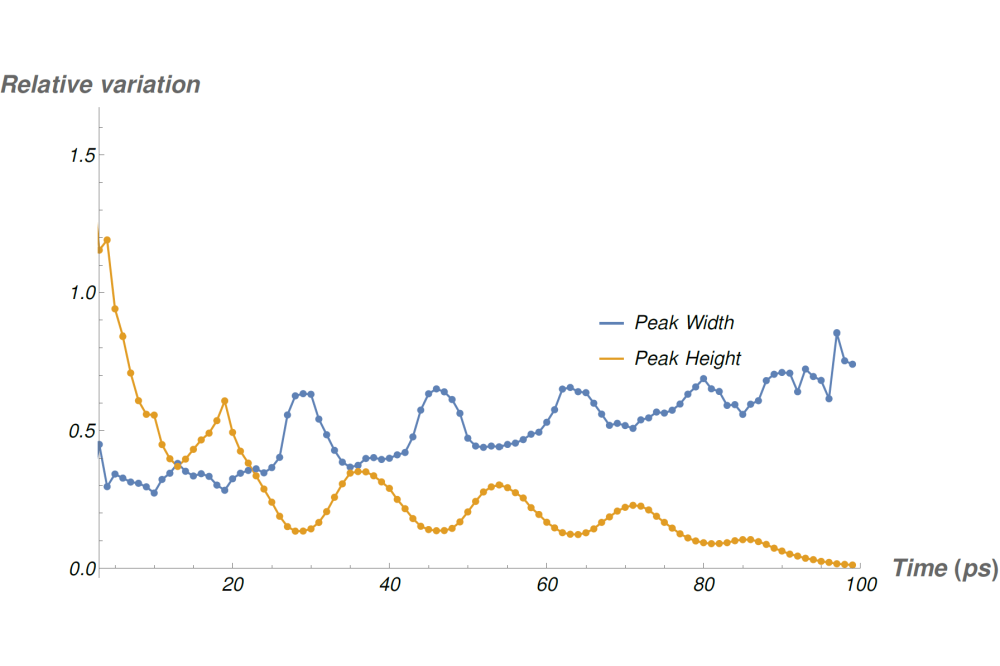
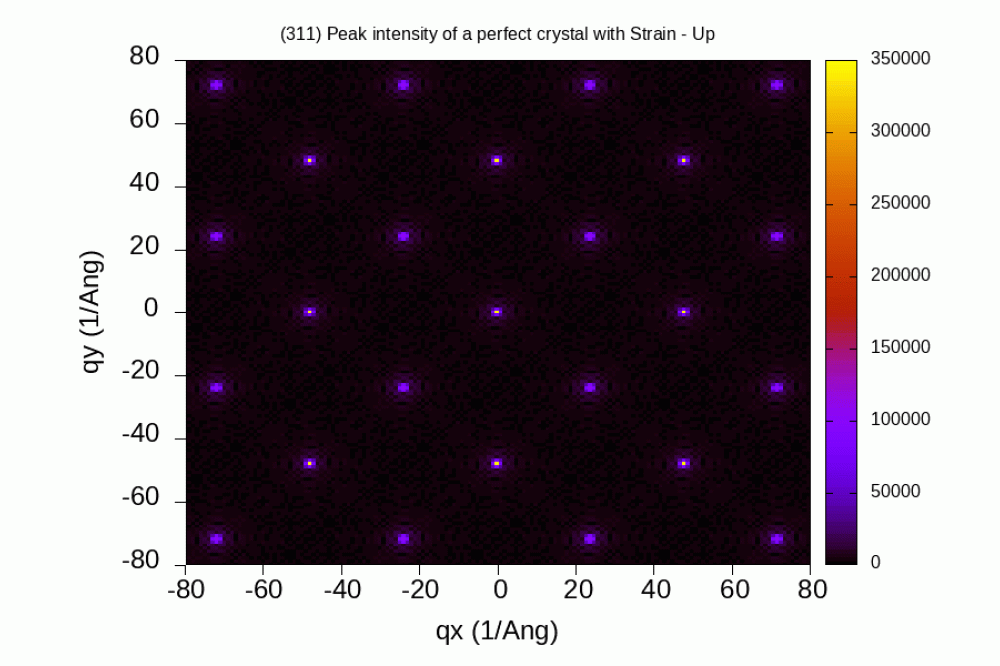
During this project we were able to theoretically interpret the Bragg peaks broadening. We also successfully simulated the evolution of the gold sample that had similar dynamics as in the experiment. We had a good agreement between the theoretically calculated Bragg peaks' width and height, and the ones obtained from the experimental data. Finally, we also explained why the same effect is diffcult to get for the polycrystalline sample.
Discussion
Thanks to the simulations that were performed on the HPC, we have understood that the origin of the diffraction peak broadening is due to a combination of strains generation inside the sample and crystallite size contributions. Upon laser irradiation, if the lattice heating rate is lower than the mechanical relaxation rate of the material, then this will lead to the generation of pressure waves inside the sample. Initially, this pressure is homogeneous and behaves as a standing wave. However, due to random generation of liquid nano-droplets in the sample, the pressure wave is then scattered. This induces a nonuniform lattice spacing which is finally translated as an oscillation in the width and height of the Bragg peaks. This explains the experiment with good aggreement. For the polycrystalline case, the melting fronts always start from the grain boundaries, this entails a considerable deformation of the sample and thus the shadowing of oscillation in the peak's width.