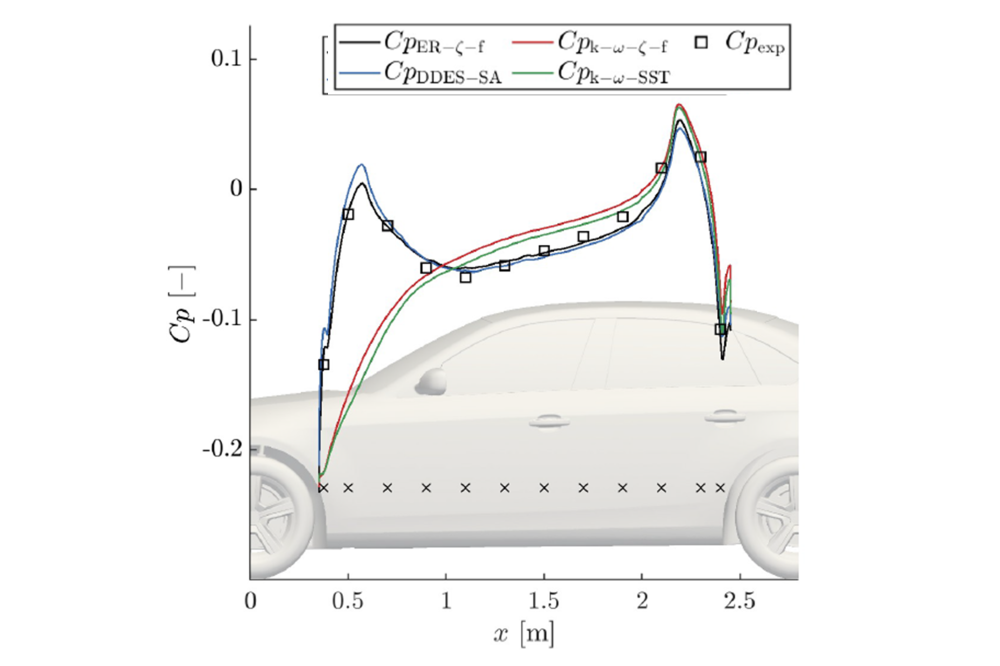
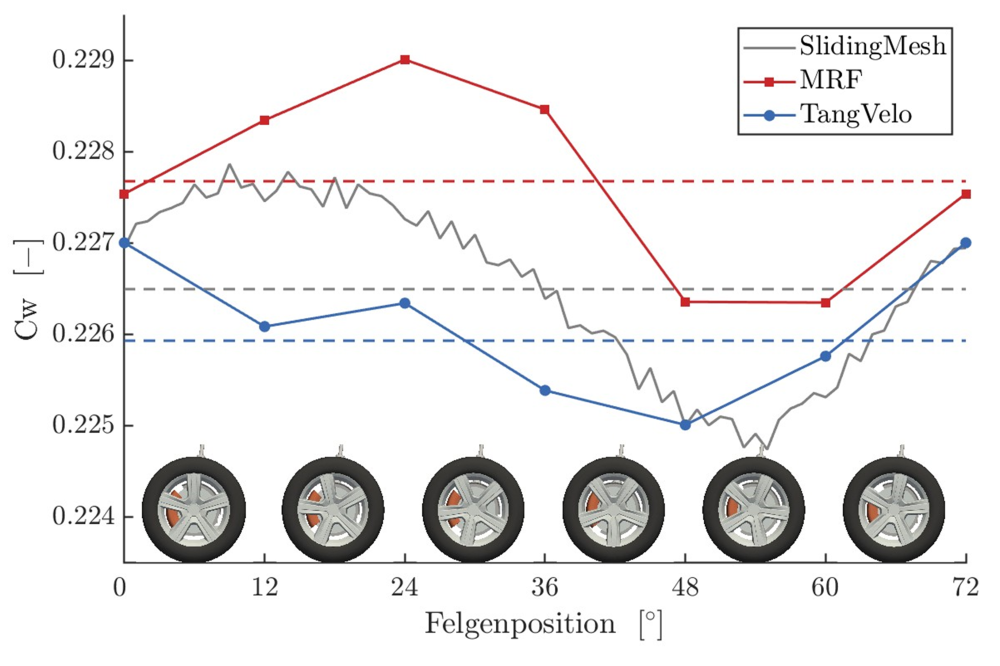
With respect to the choice of turbulence models, simulation results clearly point to the predominance of eddy-resolving methods, which tend to outperform the RANS models in both the prediction quality of first- and second-order statistics, especially in the zones of separation and high anisotropy. This is best illustrated in Figure 2, where the typical simulation outcome - pressure distribution around the car side surface is shown for two RANS and two ER models (as a baseline, sliding mesh approach is used in all cases for maximum physicality). Symbols denote the measured pressure coefficient, supplied from the experiment. This position is especially relevant due to the complex flow conditions established around the wheel, involving separations, secondary flows, as well as high level of anisotropy. As can be seen in the Figure 2, both eddy-resolving (ER) models are able to correctly capture the pressure distribution, despite the underlying difference in modeling formulation. On the other hand, both (U)RANS models predict a zone of substantially smaller pressure in comparison with experiment. This is especially relevant in the vicinity of the rotating wheel, where the complex flow conditions are established. Further downstream, flow becomes attached and all models perform with similar accuracy. Increase in accuracy with usage of eddy-resolving models can be attributed to the partial resolution of the spectrum, where the most energetic coherent structures, associated with the complex flow conditions are directly resolved. Hence, it can be concluded that the usage of eddy-resolving models clearly has advantages in terms of accuracy, despite the increased computational effort. Once the predominance in eddy-resolving models is established, further studies involving the accuracy of wheel rotation strategies are conducted. With ER-k-ω-ζ-f model taken as a baseline parameter, it was observed how the drag coefficient changes along the wheel rotation. This is shown in Figure 3. First, the phaseaveraged value of drag coefficient along the one full symmetric wheel rotation (72°) is observed. For sliding-mesh method, the sinusoidal change is clearly observed, whereas variations around the mean reach 2 to 3 points. As for other two competing methods, they can not be compared directly in one simulation case, since the mesh is completely stationary. However, it is possible to perform multiple simulations involving stationary mesh in which the wheel is rotated by a fixed number of degrees, until the symmetry point is reached. In total, 6 different cases were studied with stationary mesh. Results are compared with the sliding-mesh method in Figure 3. As can be seen, both methods lead to the quantitatively similar integral results, whereas the apparent sinusoidal change in drag coefficient is identified for all three methods. Deviations between the mean values also do not exceed 2 to 3 points in terms of pressure coefficient. Although this study shows that the methods of lesser complexity can also be used for reproducing the integral aerodynamic characteristics of the vehicle, by performing multiple simulations with continuously changing (but stationary) geometry, it is also bound with additional computational effort which doesn’t justify its use. Conclusions following the performed simulations show that the increase in simulation accuracy can be achieved by using the turbulence models capable of adequately resolving the turbulent spectrum, as well as methods which directly capture the effect of wheel rotation.