When to Trust Your Model in Model-based Value Expansion?
Introduction
Model-based value expansion methods promise to improve the quality of value function targets and, thereby, the effectiveness of value function learning. However, to date, these methods are being outperformed by Dyna-style algorithms with conceptually simpler 1-step value function targets. This shows that in practice, the theoretical justification of value expansion does not seem to hold. We provide a thorough empirical study to shed light on the causes of failure of value expansion methods in practice which is believed to be the compounding model error. By leveraging GPU based physics simulators, we are able to efficiently use the true dynamics for analysis inside the model-based reinforcement learning loop. Performing extensive comparisons between true and learned dynamics sheds light into this black box. This paper provides a better understanding of the actual problems in value expansion. We provide future directions of research by empirically testing the maximum theoretical performance of current approaches.
Methods
We adapt Model-based Value Expansion (MVE) for the maximum-entropy reinforcement learning case in order to combine it with a model-free Soft Actor-Critic (SAC) learner. The main objective of maximum-entropy RL is to find a policy that maximizes the entropy regularized discounted reward a crucial point is to learn a good value function. We leverage a learned dynamics model to approximate value function targets by expanding the targets using modeled trajectories. Our reliance for GPU accelerators and the need for large ablation studies on multiple seeds and across different configurations makes this project computationally very demanding.
Results
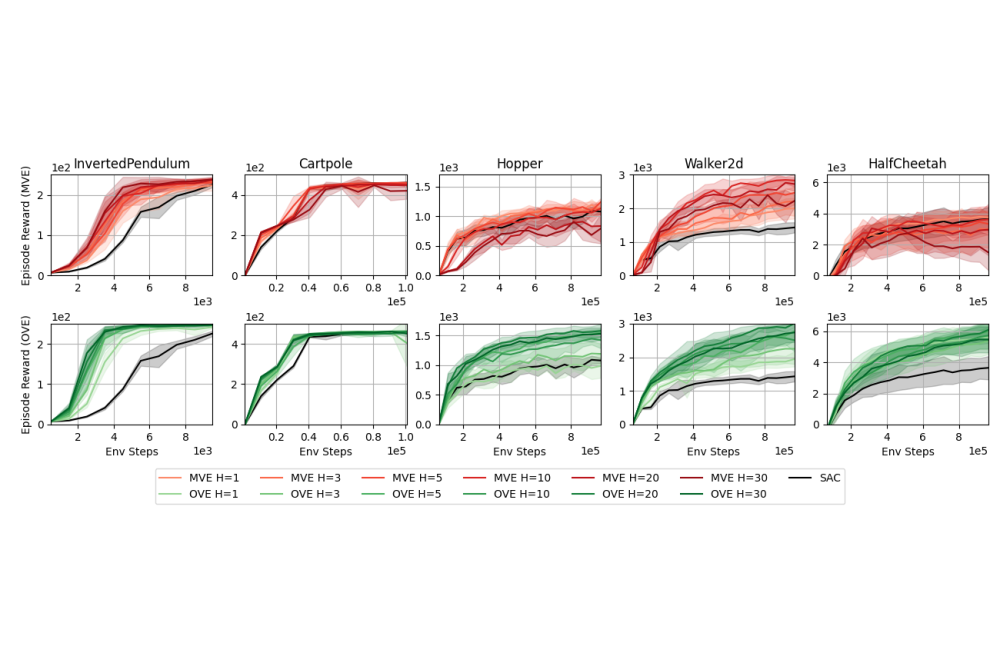
Our experiments have empirically shown that in the absence of model errors, MVE shows increased performance with longer rollout horizons. Therefore, we conclude that MVE can be made more sample efficient by training more accurate dynamics models. At the same time, we have seen diminishing returns of that improvement with increasing rollout horizons. Our empirical findings strengthen the theoretical justifications of MVE.
Discussion
Our empirical results allow for two streams of future research. First, improving model accuracy through better model training techniques and architectures. Second, understanding how model errors impact value expansion and how the negative impact can be mitigated. This needs more research into analyzing and understanding how these model errors negatively impact training. In the future, we plan to take a detailed look at the exact nature of the impact of model errors on the learning process and on the generated value targets themselves. We hope that by understanding the effects, we can design more capably algorithms that are more robust to model errors and sample efficient at the same time.