Ab-initio Description of p-shell Hypernuclei
Introduction
Hypernuclei are atomic nuclei that contain other baryons apart from nucleons (protons and neutrons). These other baryons, called hyperons, contain Strange quarks, the third-lightest quark flavor, in addition to light up and down quarks. Hypernuclei have been produced in accelerator experiments for over 50 years and despite their very short lifetimes lots of data on their properties have been collected[1] . Another site where hyperons and hypernuclei are believed to exist are neutron stars. Hence, understanding the interactions of hyperons among each other and with nucleons is crucial for the understanding of these stellar objects. Additionally, hyperon-nucleon interactions provide a generalization of nucleon-nucleon interactions that can be used to test models of these forces and explore the symmetries that link the models back to Quantum Chromodynamics (QCD), the theory of the strong force that binds nuclei and the baryons themselves. In order to really test our understanding of these forces, we need calculations of hypernuclei which results we can compare to experimental data.
Methods
The method for solving this many-body problem should make no assumptions on the structure of the hypernucleus, so that the results only depend on the interaction models used in the calculation. The class of many-body methods that fulfills this requirement is the class of ab initio methods and, until recently, these methods were applicable to systems of five or less baryons, limiting the accessible range to only a handful of hypernuclei. Our group has developed a computer code that uses the Importance-Truncated No-Core Shell Model (IT-NCSM) to solve the hypernuclear many-body problem allowing us to calculate systems consisting of up to approx. 16 baryons and thus dramatically increasing the number of accessible hypernuclei[2]. With this code we did calculations for a small set of hypernuclei and we can demonstrate that different models of the hyperon-nucleon interaction give very different results when applied to many-body systems, although they fit the data from the two-body system equally well.
Discussion
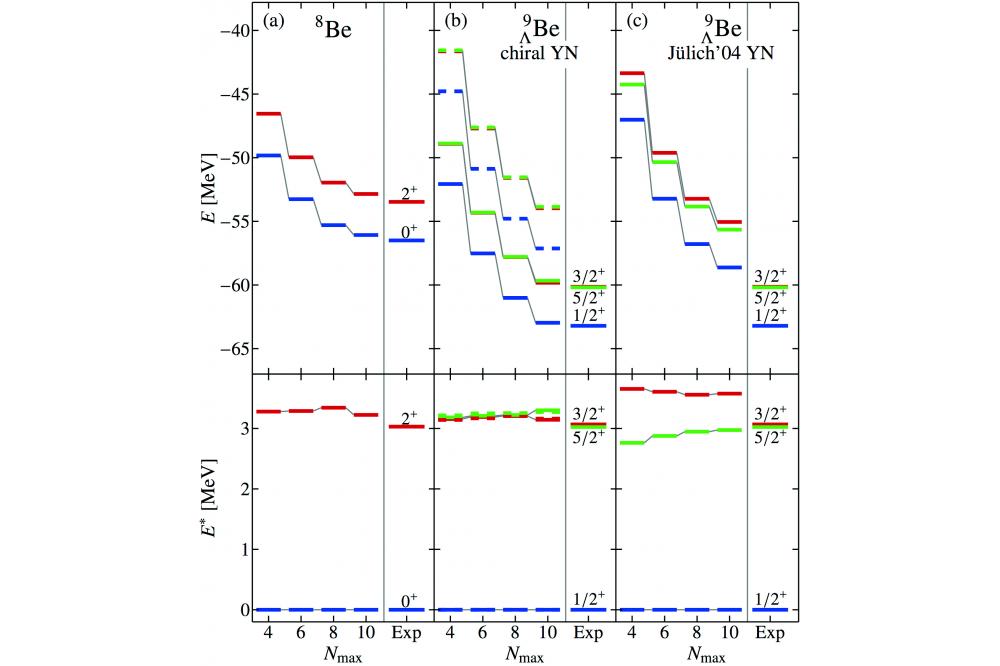
As an example we show in fig. 1 the ground-state energy and spectrum of Λ 9Be calculated with a modern interaction resulting from a systematic expansion based on the symmetries of QCD (chiral YN) and with a modern meson-exchange interaction (Jülich‘04). The chiral interaction predicts the excited-state doublet to be almost degenerate, while the Jülich‘04 predicts a very large splitting. Also, depending on the interaction, the predicted ground-state energies range from slightly too low to slightly too high. These discrepancies originate in the hyperon-nucleon interaction, they do not stem from the nucleonic part because the parent nucleus (the nucleus that one gets after removing the hyperon from the system) is reproduced well by the interactions we employ. In conclusion, our calculations provide additional constraints that are vital to further the understanding of baryon-baryon interactions.
Outlook
In the near future we will extend our calculations to a survey of hypernuclei throughout the applicable range. We also plan to extend the code so it can include hyperon-nucleon-nucleon three-body terms that either arise naturally during the expansion of the interaction or are induced by the procedure we employ to improve convergence of the many-body calculation.