Andauernde Weiterentwicklung eines Frameworks für numerische Simulationen auf Basis von Discontinuous Galerkin-Methoden
Introduction
In den Ingenieurswissenschaften tritt eine Vielzahl von Problemstellungen auf, welche sich nur durch partielle Differentialgleichungen realitätsnah beschreiben lassen. Die wohl bekanntesten Vertreter dieses Gleichungstyps sind die Maxwell-Gleichungen zur Beschreibung von elektromagnetischen Feldern, die Schrödinger-Gleichung zur Beschreibung von quantenmechanischen Systemen und die NavierStokes Gleichungen der Strömungsdynamik. Alle diese Beispiele besitzen die Gemeinsamkeit, dass für praxisrelevante Geometrien und Materialparameter keine exakten Lösungen bekannt sind, so dass diese im Rahmen von numerischen Simulationen auf einer Gitterbeschreibung des Problems annähernd berechnet werden müssen. Sowohl die Genauigkeit als auch der Rechenaufwand einer solchen Simulation wird maßgeblich durch das verwendete Diskretisierungsschema und die Auflösung bestimmt.
Methods
Unter Auflösung versteht man hierbei die Anzahl der Gitterpunkte in Raum und Zeit, welche im Kontext der Strömungsdynamik im übertragenen Sinne als „Messpunkte“ für die lokalen Geschwindigkeiten und den Druck verstanden werden können. Von zentralem Interesse bei solchen Verfahren ist die Konvergenzrate, welche die Abnahme des Fehlers bei einer Verfeinerung des Gitters beschreibt. In der Industrie werden zurzeit hauptsächlich Verfahren mit quadratischer Konvergenz eingesetzt, d.h. durch die Verdopplung der Auflösung in jede Raumrichtung wird der Fehler um den Faktor 4 (=22) reduziert. Anderseits wächst der Rechenaufwand für dreidimensionale Simulationen in diesem Fall mindestens um den Faktor 8 (=23), so dass sehr schnell die Grenzen des technisch machbaren erreicht werden. Am Fachgebiet Strömungsdynamik werden aus diesem Grunde seit einiger Zeit sog. Discontinuous Galerkin-Methoden eingesetzt, welche prinzipiell beliebig hohe Konvergenzraten erreichen können. Auch hier steigt der Rechenaufwand unter Gitterverfeinerung natürlich um den gleichen Faktor, aber der Zugewinn an Genauigkeit ist bei weitem größer (Abbildung 1). Zusätzlich zum Berechnungsaufwand spielt insbesondere im wissenschaftlichen Kontext der Implementierungsaufwand eine nicht zu vernachlässigende Rolle, da die Verwendung von Supercomputern erhebliche Anforderungen an die Fähigkeiten der Programmierer stellt. Um verschiedene Problemklassen und Lösungsansätze mit minimalen Mehraufwand behandeln zu können wird am Fachgebiet Strömungsdynamik daher seit einigen Jahren das Software-Framework BoSSS (Bounded Support Spectral Solver) stetig weiterentwickelt [1-9]. Das Framework erlaubt es Ingenieuren mit geringen Vorkenntnissen im Bereich der Software-Entwicklung in kürzester Zeit leistungsfähige, problemspezifische Applikationen zu implementieren.
Results
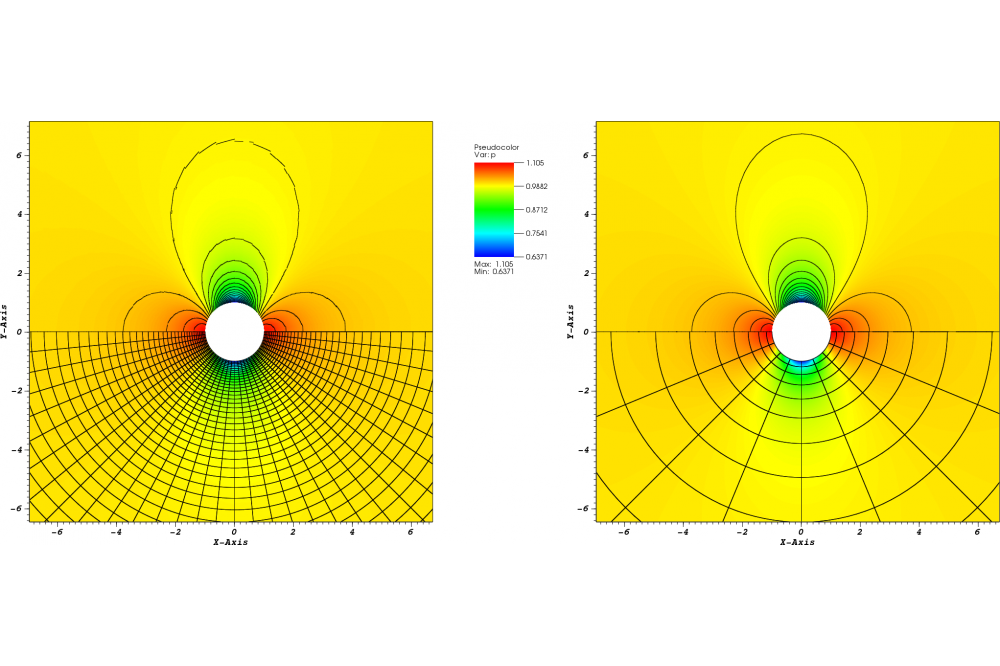
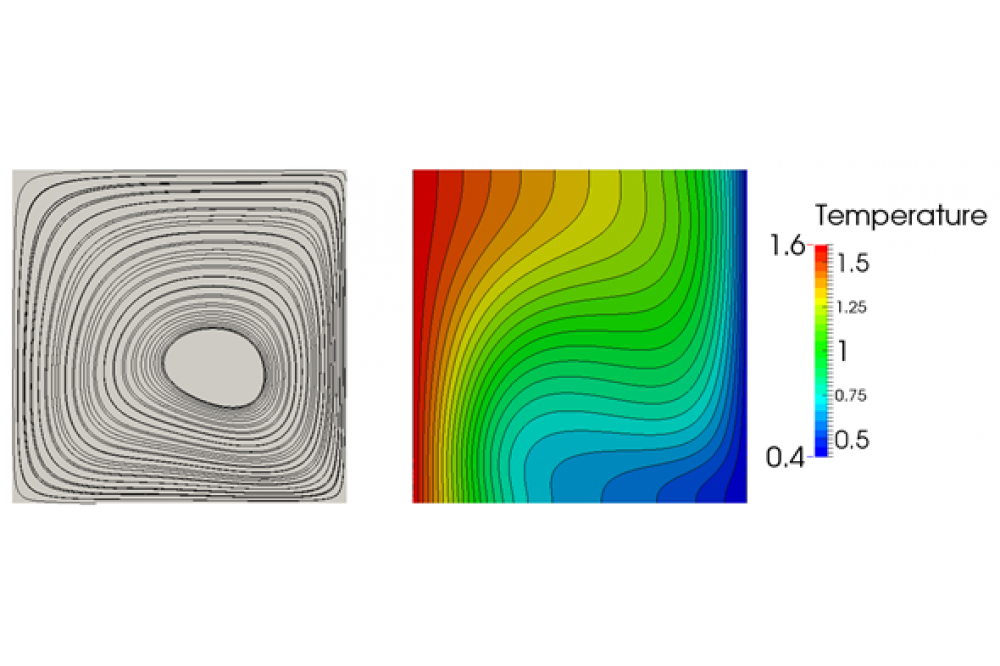
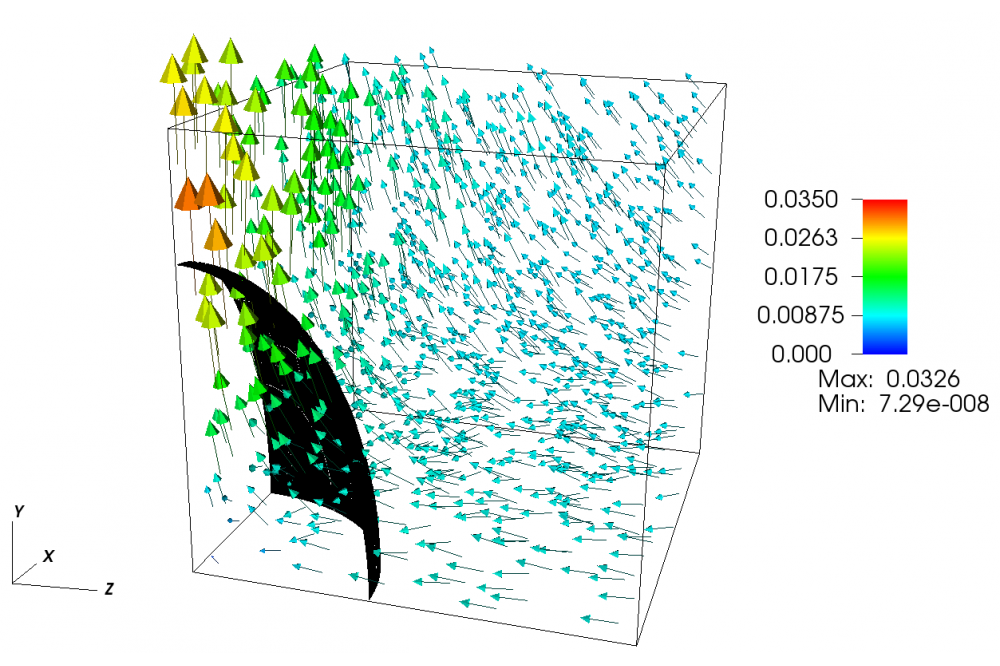
Auf Basis dieses Frameworks konnten inzwischen Lösungsalgorithmen für eine breite Klasse von Problemen entwickelt und mit Hilfe des Lichtenberg-Hochleistungsrechner anhand von geeigneten Testfällen verifiziert werden. Ein klassisches Beispiel ist die dreidimensionale Umströmung von Festkörpern mit inkompressiblen Medien wie Wasser (Abbildung 2), welche als Startpunkt für physikalisch anspruchsvollere Anwendungen gesehen werden kann. Beispiele sind die Simulation von Strömungen, die sich aufgrund von temperaturabhängigen Materialparametern (wie Dichte und Viskosität) in flüssigen Medien einstellen (Abbildung 3), sowie die Untersuchung des Einflusses von starken elektrischen Feldern auf Wassertropfen (Abbildung 4), welche für die Lebensdauer von Hochspannungsisolatoren eine maßgebliche Rolle spielen.