Importance-Truncated Valence-Space Shell Model and Energy-Variance Extrapolation
Introduction
In nuclear structure theory, models have been developed which describe nuclear properties precisely. One well established model is the valence-space shell model, which provides access to spectra and other observables of a wide range of nuclei. The results show remarkable agreement with experimental data where available and can be used to make quantitative predictions.
Methods
We extend the shell model to model spaces and nuclei beyond the reach of the conventional shell model. In the shell model, only nucleons occupying orbits on top of an inert core are treated as active degrees of freedom. This implies the definition of a suitable model space constructed from the single-particle states of the valence nucleons and an effective interaction adapted to it, accounting, e.g., for the influence of core on valence nucleons. Eigenstates of the system are obtained by constructing and diagonalizing the Hamilton matrix, which is computationally demanding (typical matrix dimensions are of the order of 109). The model space sizes grow combinatorially with the number of valence orbits and the number of valence nucleons.
Results
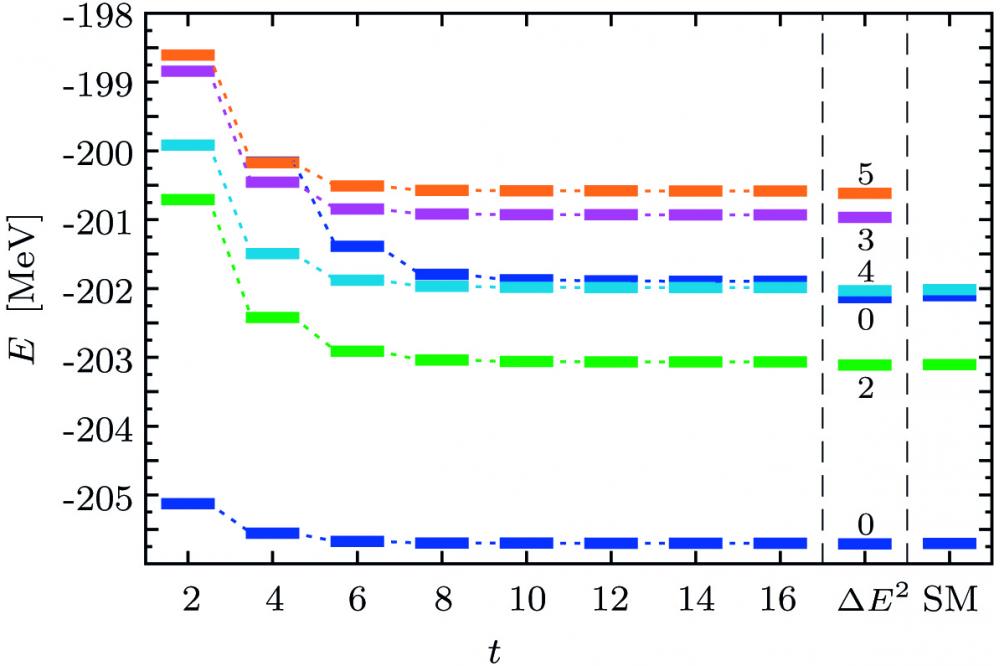
To overcome these limitations, we introduce an importance-truncation scheme to the shell model. This approach has already been applied successfully to nuclear structure theory in the no-core shell model. [1] It is based on the assumption that many of the basis states in the model space are dispensable for the description of a few low-lying target eigenstates. By employing an importance measure derived from perturbation theory, we estimate the relevance of the individual basis states for the target eigenstates and reduce the model space significantly by considering only the important basis states for the computationally demanding construction and diagonalization of the Hamilton matrix. In this way, the quality of the results remains almost unchanged, but the applicability of the shell model is extended to larger model spaces and a greater variety of nuclei. For our calculations, we have developed a highly optimized hybrid MPI code that constructs the basis and calculates and diagonalizes the Hamilton matrix efficiently.
Discussion
The importance-truncated shell model (IT-SM) accounts approximately for basis states excluded from the model space by an extrapolation to vanishing importance threshold. We estimate the uncertainty of the extrapolated energy by repeating the extrapolation using different fit functions. Both, energies and observables, e.g. quadrupole moments or transition strengths, can be calculated in remarkable agreement with the exact values. However, this extrapolation scheme suffers from the fact that no physical model is available for the fit function. In some cases, this can be reflected in a large extrapolation uncertainty. For the energies, a more reliable extrapolation based on the energy variance can be carried out. The energy variance provides a measure for the quality of an approximate eigenstate and vanishes in the limit of the exact eigenstate. We exploit this property by calculating the energy variance for the IT-SM energies and extrapolating to vanishing energy variance. As proposed in (Mizusaki and Imada),[2] we use a quadratic function for the fit, which has been shown to reproduce the exact energies precisely. The energy-variance extrapolation corrects, in principle, for effects of the different truncations employed in the IT-SM.