Nuclear Matter in the Parity Doublet Model with Fluctuations
Introduction
Strong-interaction matter fuels the stars and makes up almost the entire mass of the luminous universe. The underlying theory of quarks and gluons, Quantum Chromodynamics (QCD), completely specifies these interactions, which are so complex and non-linear that they have not yet to be fully understood. Indeed, it is these strong interactions that under normal conditions confine quarks and gluons into the interior of hadrons. Understanding the generation of their masses, the confinement of quarks and gluons, the different phases of QCD at extreme temperatures or densities and the transitions between them are some of the great challenges in physics.
Methods
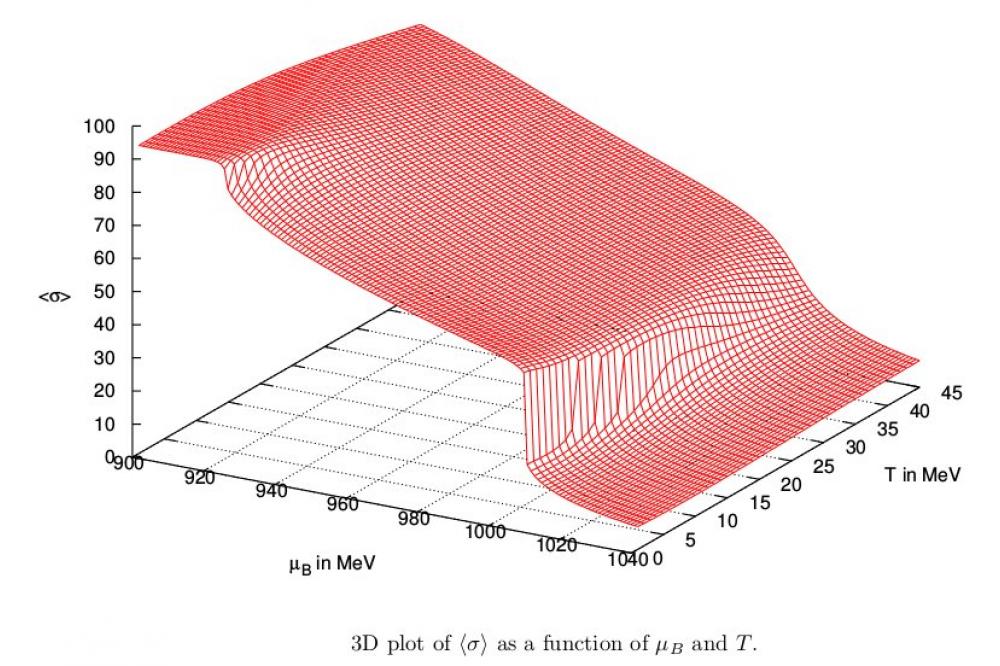
Of particular interest is the behavior of QCD matter at extremely high densities, as they exist, for example, in the interior of neutron stars. These are described by introducing the baryon chemical potential which prevents direct studies of dense baryonic matter in QCD by ab-initio Monte-Carlo simulations due to the fermionsign problem. An alternative non-perturbative method without this problem is provided by the Functional Renormalization Group (FRG). At temperatures below 20 MeV nuclear matter forms in a first-order phase transition analogous to the condensation of water vapor. In a relativistic description, this liquid-gas transition occurs at a critical value of the baryon chemical potential of 923 MeV which is about 16 MeV below the rest mass of the nucleon, corresponding to the binding energy per nucleon of nuclear matter. Here, we study the nuclear matter transition using the Parity Doublet Model with fluctuations as described by the FRG. From a technical point of view our calculations require the numerical integration of a flow equation which can be reduced to integrate a high-dimensional differential equation on a grid in field space over a multi-dimensional parameter space. This flow integration is followed by a minimization with respect to the fields. This procedure has to be repeated for a range of values in order to study the phase structure of the model. Depending on the size of the grid in field space this can require a large amount of computing power, but the calculations can trivially be parallelized and making the problem feasible for multi-core calculations to be performed on a CPU cluster (in our case the Lichtenberg-cluster). For the numerical integration the GNU Scientific Library (GSL) is used in combination with Open-MPI for the multi-core implementation on a CPU cluster. The characteristic physical quantity to investigate the nuclear matter transition is the chiral condensate. It is extracted from the above-mentioned calculations as the minimum with respect to one of the field directions. This condensate is shown as a function of baryon chemical potential and temperature in the figure.
Results
The discontinuities at low temperatures indicate two distinct first-order phase transitions which get weakened with temperature until they eventually disappear in critical endpoints. The model is capable of describing the liquid-gas transition of nuclear matter together with a chiral symmetry restoration transition at even higher baryon chemical potentials. Although we observe rather strong quantitative modifications due to the fluctuations, as compared to existing mean-field studies, the qualitative description is quite compelling.
Outlook
Future extensions will include explicit quark degrees of freedom with wave-function renormalization to avoid double counting of quarks and hadrons in a Quark-Meson-Baryon model possibly with additional Polyakov-loop variables to incorporate confinement. These extensions will require even larger amounts of computing resources in the future. They will be crucial to arrive at a more concise description of strong-interaction matter in the high net-baryon density region of the QCD phase diagram.