Computational Modelling of Plasma-Actuated Flow Control by Means of Eddy-Resolving Turbulence Models
Tarik Čorbo_Computational Modelling of Plasma-Actuated Flow Control by Means of Eddy-Resolving Turbulence Models_Figure1Figure 1: Simulated area (left) and working principle of the plasma actuator (right)[1].
Tarik Čorbo
Tarik Čorbo_Computational Modelling of Plasma-Actuated Flow Control by Means of Eddy-Resolving Turbulence Models_Figure2Figure 2: Velocity profiles for the steady PA force computations at different locations in compari-son with the experimental measurements from Kriegseis et al..(top). Velocity profiles obtained from the simulations using a time-varying PA force at different locations compared to the experimental measurements from Kriegseis et al..(bottom)[1].
Tarik Čorbo
Tarik Čorbo_Computational Modelling of Plasma-Actuated Flow Control by Means of Eddy-Resolving Turbulence Models_Figure3Figure 3: Streamwise Reynolds stress component fields for the simulations using a neural network trained on linearly interpolated data to determine the time-varying PA force (top) and using the steady PA force (bottom)[1].
Tarik ČorboIntroduction
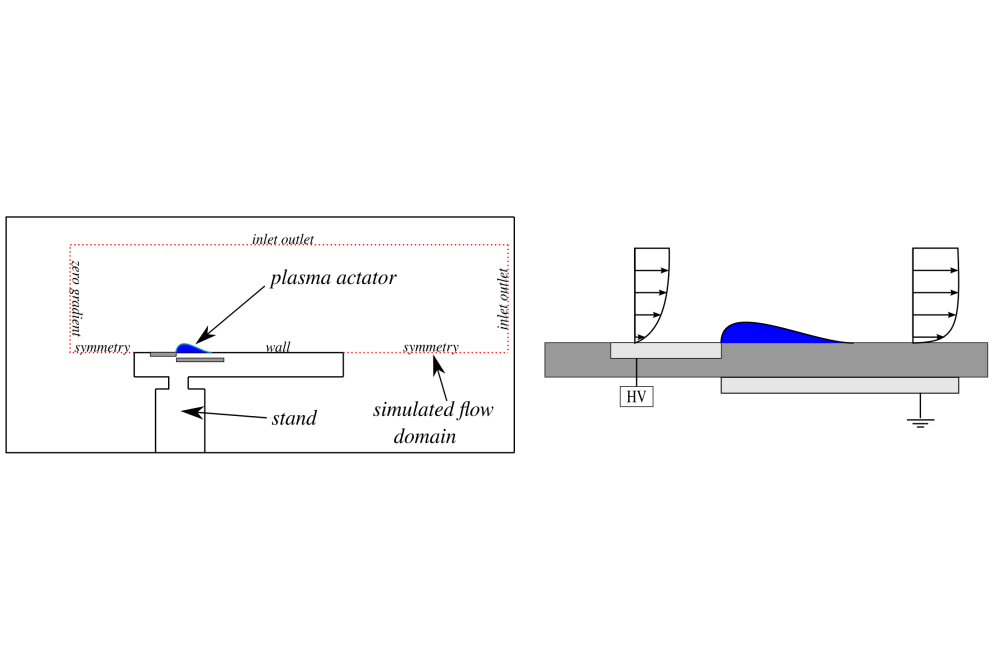
Plasma actuators, Figure 1, represent flow control devices that have no moving parts and that work by ionizing the air in their close proximity. These ions are then accelerated in the presence of the electric field and also cause non ionized particles to start moving. Accurately modeling this force that they produce allows for the simulation of flows where they are present by the use of CFD. Two approaches to the modeling of the transient plasma actuator force were tested in this work. The first relies on the measurements by Kuhnhenn et al., utilizing the force values measured at eight time points during an AC discharge cycle of the plasma actuator. The second approach uses these same eight measurements along with additional interpolated force values to train a neural network that can predict the force at any spatial and temporal position. These models are tested on the flat plate case, Figure 1, in conjunction with the Improved Instability Sensitive Reynolds Stress Model, an eddy resolving turbulence model. Additionally, the previous steady plasma actuator force approach is used for the validation as well as experimental measurements of the flat plate case from Kriegseis et al..[2],[3].
Methods
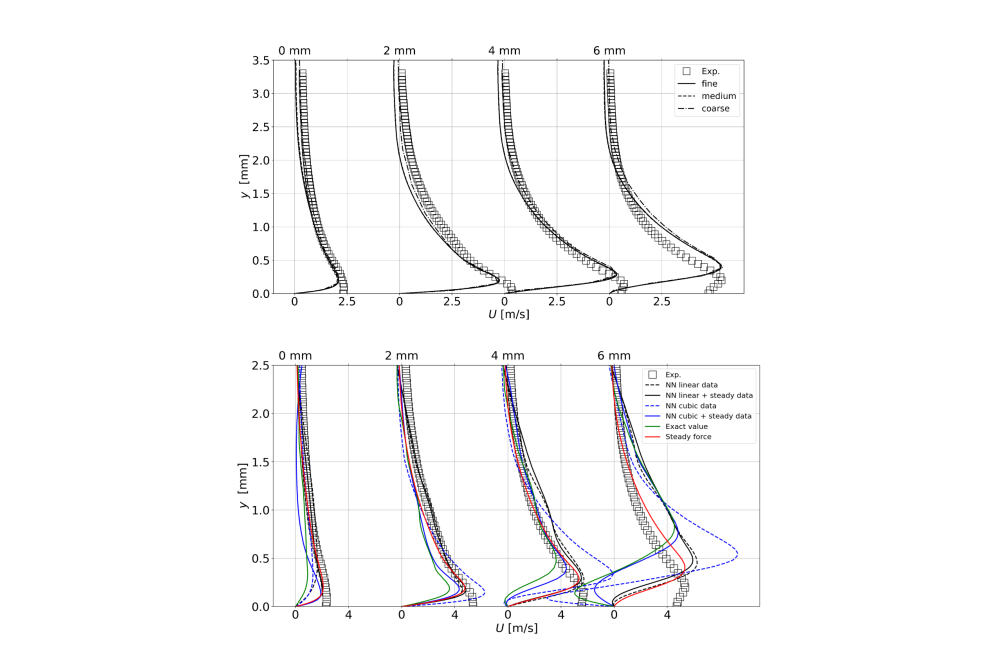
All the simulations are performed using the C++ Library OpenFOAM®. The equations to close the continuity and momentum equations are additionally implemented into the code. Second-order accuracy is ensured for both the spatial and temporal derivatives. A variable time step is used for all simulations, with the constraint of CLF<0.7, except the ones using the first approach to model the unsteady plasma actuator force which require a constant timestep that corresponds to the measurement frequency. Both of the modeling approaches for the unsteady plasma actuator force are also implemented into the solver. Three different meshes are tested with 1.85, 0.8 and 0.4 million cells using the steady force model and the middle mesh is chosen for all other simulations, Figure 2(top). Multiple neural network configurations were tested and the final one that was chosen consists of six hidden layers. The training data for the neural networks consisted of the eight original force measurements as well as additionally interpolated values. Two interpolation methods were used: a cubic and linear method. Additionally, neural networks were trained using the original measurements of the time varying force and cubically or linearly interpolated data as well as the average force that was measured byKriegseis et al..[2],[3].
Results
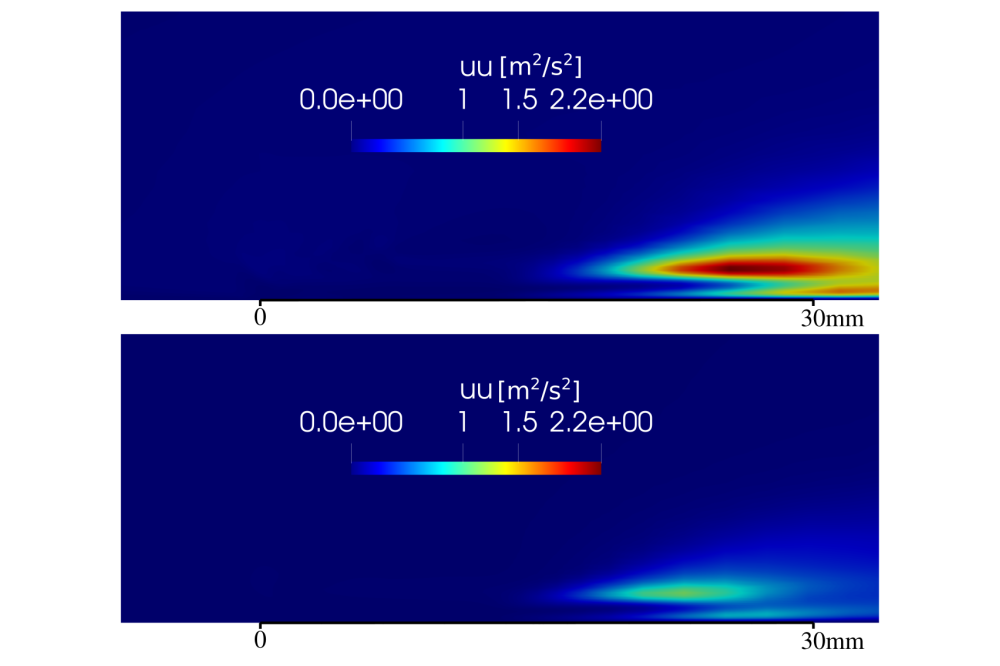
The velocity profiles for the different force models tested are shown in Figure 2(bottom) at different locations where 0 mm corresponds to the end of the exposed electrode. From the figure it is clear that the best results are obtained from the neural network trained on linearly interpolated data with the addition of the averaged force measurements, where the agreement is the closest to the steady force simulations and experimental measurements. Another important note is the improvement obtained by incorporating the averaged force measurements into the training. This leads to a clear improvement compared to the force model that is trained only by the interpolated data. Additionally, by looking at the Reynolds stress component fields obtained from the unsteady force model trained on linearly interpolated data and obtained from the measured averaged force, Figure 3, it is clear that there is an additional production of turbulence which is also important to capture and which is not possible by using only an averaged force in the simulations.
Discussion
The focus of this research was the development and validation of an unsteady plasma actuator force model. Two different approaches were tested and of the two approaches the most promising results were obtained by using experimental measurement data of the unsteady plasma actuator force along with linearly interpolated data gave the best results. Further work will focus on fine tuning the model and the calculation of more complex cases to further validate it.
