Direct Numerical Simulations of Mesopore Imbibition Using a Phase-Field Approach
Introduction
Mesoporous materials, which have pore sizes in the range of 10-200 nanometers, have attracted significant attention due to their unique physical and chemical properties and potential applications in various fields. However, the mechanisms governing liquid film imbibition in mesopores are not fully understood. To gain a deeper understanding of the forces influencing imbibition, this work conducts direct numerical simulations of a non-miscible, isothermal two-phase system within a capillary with a constant diameter at the mesopore size scale. The modeling focuses on various parameters: the pore radius, the influence of contact-line friction, and the equilibrium contact angle at the three-phase contact line.
Methods
The study utilizes the open-source C++ library OpenFOAM®. The used in-house solver is designed for phase-field multiphase flow, specifically addressing the coupled Cahn-Hilliard Navier-Stokes equations. This multiphase solver, named as phaseFieldFoam, is developed within the OpenFOAM framework (FOAM-extend 5.0). Within this framework, phase-field methods are applied to depict the interface between two fluid phases. This representation considers the interface as a gradual transition across a narrow region, achieved by continuously adjusting the phase-field order parameter (or volume fraction) from one phase to the other. It is noteworthy that the movement of the interface is influenced by the gradient in the local chemical potential, providing a natural regularization of stress singularities at the moving contact line.
Results
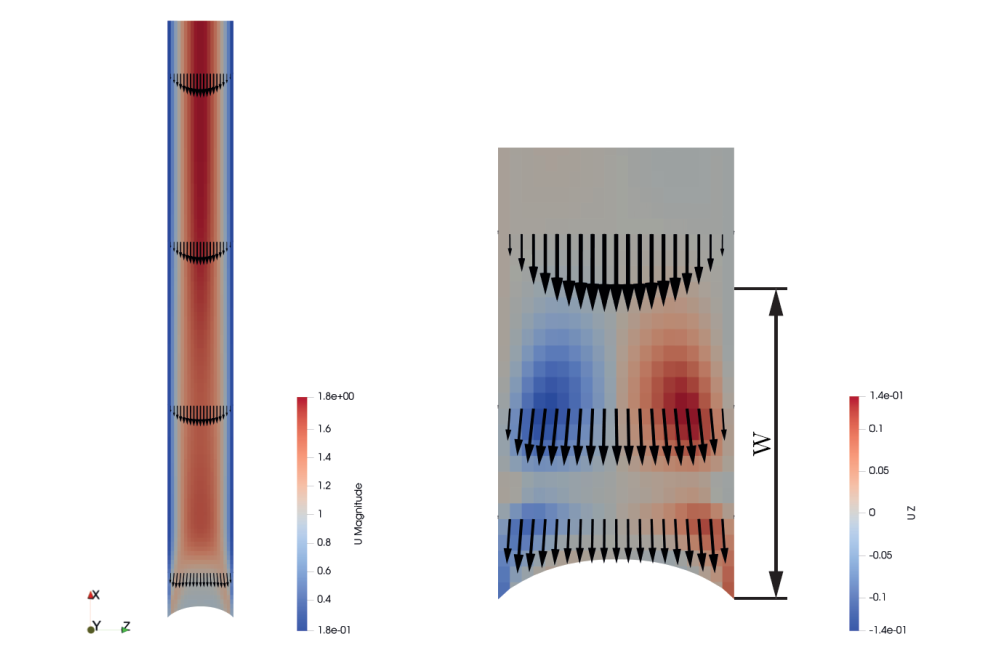
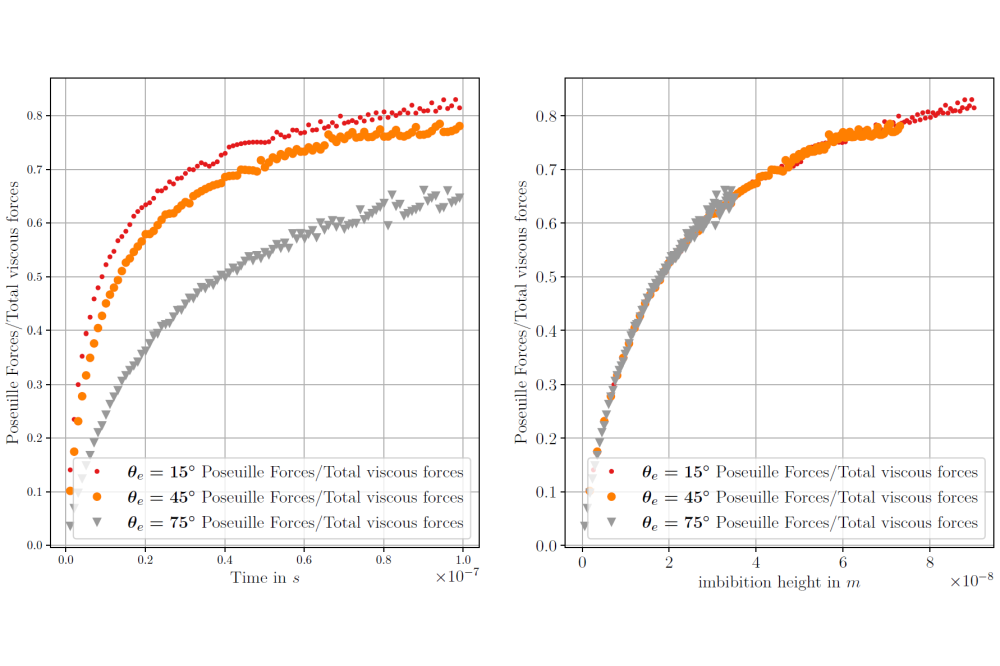
Results of the liquid film height over time are compared to the well-known Lucas-Washburn equation. We see that the motion of the film height at the early-stages of imbibition does not follow the assumed z ∼ t1/2, but instead, it follows a linear fit (z ∼ t), shown in Figure 1. By computing the forces that play a role during the imbibition process we see that the force that arises due to the meniscus formation is much greater than the viscous force coming from the liquid column (Poiuseille force), early on. By plotting the the ratio between the meniscus force and the total viscous forces, we can see when the transition (crossover) between the linear and Lucas-Washburn regime happens. We observed that the contact angle has negligible effect of where this crossover happens, which was only shown analytically. On the other hand, we see that the radius plays a considerable role of where this crossover happens. Contact line friction effects were also studied, but results show that this force also is negligible to the crossover length.
Discussion
Furthermore, this linear regime is observed for all studied contact angles, where the lower the contact angle, the faster the transition into the Lucas-Washburn regime occurs. This is due to the higher capillary force, as the liquid column imbibes into the pore much quicker than for cases with higher contact angle, and as such the viscous drag force quickly overtakes the dissipation force caused by the changes in dynamic contact angle. Thus, the regime transition is faster. Despite this, we see that the contact angle has little effect on the position at which the switch between the linear and Lucas-Washburn regimes occur, where we find that at around z ∼ 10r the dissipative forces balance each other out (see Figure 3). We also see that changes in radius can greatly affect the transition from a linear to Lucas-Washburn growth rate, where a larger radius leads to considerably large crossover lenghts (z ∼ 1000r). Our work also highlights the usage of DNS using phase-field methods as a viable pathway for investigating nano and mesoscale imbibition processes, in junction with experimental work and molecular dynamic simulation. Systematic comparisons between phase-field methods and molecular dynamics have been done previously, which show the potential that phase-field approach also works on the atomistic scale.
Outlook
For future work, other setups could also be investigated, such as cases where multiple phases are present, effects of contact line friction, more complex porous geometries, phase-change, among others.