Algorithm Unfolding in Multicell Downlink MIMO Precoding
Schynol, Lukas_Algorithm Unfolding in Multicell Downlink MIMO PrecodingFigure 1: Block model of the deep network.
Lukas SchynolIntroduction
In wireless communications, beamforming is utilized for the reception and transmission of directional wireless signals through the use of multiple antennas. In the last decade, it was one of the key technologies in wireless networks to further increase data rates. However, finding “good” beamformers which maximize the possible data rate is a hard problem.
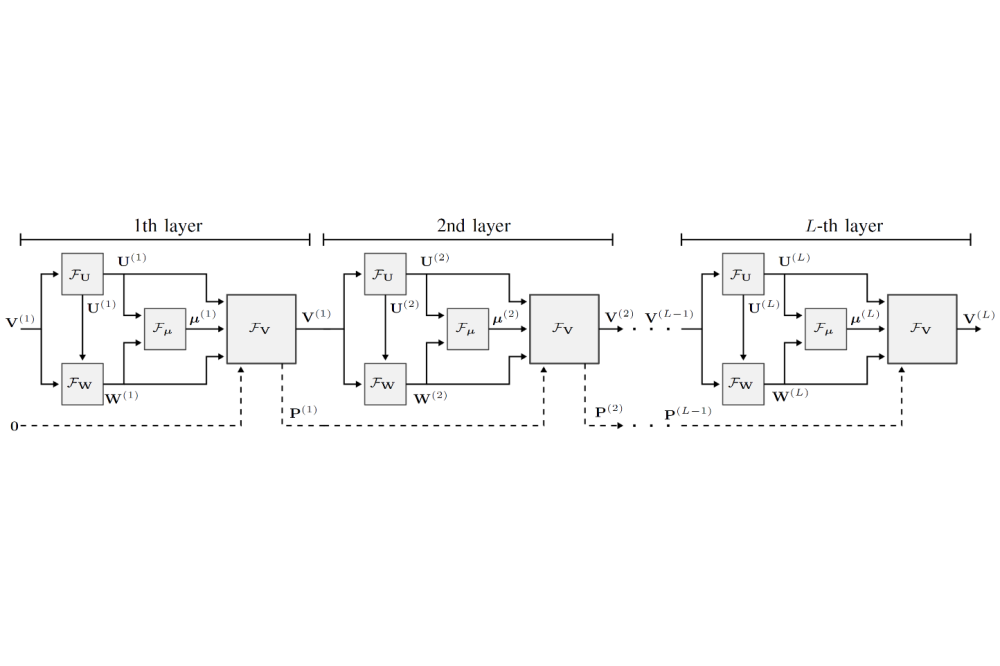
This project is concerned with finding fast and distributed methods for computing these beamformers. Recently, researchers turned to machine learning and deep neural networks for solutions. Some works in literature applied algorithm unrolling, which is the idea of deriving a trainable neural network architecture from the structure of classical algorithms. These works limited themselves in the generality of the investigated wireless scenarios. In comparison, this project is concerned developing a general architecture, which is applicable especially in the case of multiple base stations serving several users each, and which is transferable between changing wireless conditions.
Methods
We develop a deep network architecture by unrolling the classical weighted-minimum-mean-squared-error (WMMSE) algorithm. Each iteration of the WMMSE algorithm effectively translates into a deep network layer. Graph filters from the field of graph signal processing are integrated as building blocks into the layers. The filter coefficients serve as trainable weights while the architecture remains agnostic to the number of transmit or receive antennas. Further augmentations such as skip connections between layers and nonlinearities are introduced as well. The models are implemented in Python using the PyTorch library and are trained to maximize the theoretically achievable data rate given a power budget at the base stations. Training and testing data sets are generated from completely synthetic channel models as well as models obtained using ray-tracing simulations of urban environments. To evaluate the generalization and transfer learning capabilities, network models are investigated on a large number of different channel conditions.
Results
The resulting deep networks models have a low number of trainable parameters. Depending on the wireless scenario, the models require substantially fewer layers than the WMMSE algorithm requires iterations for the same performance. The deep network models adapt well to changing wireless scenario conditions, i.e., changing power budgets or noise levels as well as the number of users connected to the base stations. In addition, the model performance remains high in case of changing numbers of base station antennas or user antennas. Furthermore, the experiments show that the architecture is highly efficient with respect to training data. However, numerical issues are observed if the number of base station antennas exceeds the total number of user antennas.
Discussion
High computational gains and a considerable generalization capability of the architecture are demonstrated. The reduced number of iterations effectively reduces the communication overhead if the network is deployed in a distributed fashion. The observed numerical issues only appear in certain limited conditions and can be circumvented. However, the developed architecture is limited to beamforming with instantaneous channel knowledge, i.e., the wireless channel is assumed constant and known precisely within a time period. This condition is rarely met. Future work will, therefore, focus on probabilistic channel models.
