Bayesian Inference of Cyclic Transcription Dynamics
Introduction
Transcription is the process of converting DNA into RNA and is essential to cellular life. The transcription process consists of three phases: initiation, elongation and termination. These phases are involved in in a complex regulatory network that is still not fully understood. In the last decade, new experimental techniques such as tagging nascent mRNA with fluorescent markers have allowed to visualize transcription in live cells. Combined with probabilistic modelling, the measured fluorescence traces can be used to extract kinetic parameters such as initiation and elongation rates and shed some light on underlying regulatory mechanisms. Traditional quantitative analysis is typically based on auto correlation which is only applicable to a limited number of idealized scenarios. In this study, we develop a Bayesian inference approach that is suitable for dynamically changing transcription parameters.
Methods
We use a one-dimensional lattice to model a coarse-grained version of the DNA template. On this lattice, particles representing polymerase molecules can enter on one side, move along the lattice and exit on the right side. These transitions occur stochastically with exponential waiting time whenever the target site is vacant. As the positions of the mRNA to which fluorescent molecules attach are known, this model allows to predict observed fluorescence over time.
The discussed model is an example of a pure Markov jump process. We propose an efficient way to evaluate the log-likelihood of the model by integrating the master equation using a Krylov subspace method for matrix exponentials. The corresponding gradient with respect to the model parameters is evaluated similarly by integrating a backward master equation. Our approach was implemented in C++, parallelized with OpenMP and wrapped as a Python extension. This allows to integrate our approach into probabilistic programming languages such as Pyro. The combination with Pyro facilitates the exploration of different model configurations and gives access to powerful inference algorithms such as Hamiltonian Monte Carlo and Automatic Differentiation Variational Inference. In particular, it allows straightforward pooling of multiple traces to improve inference accuracy.
Results
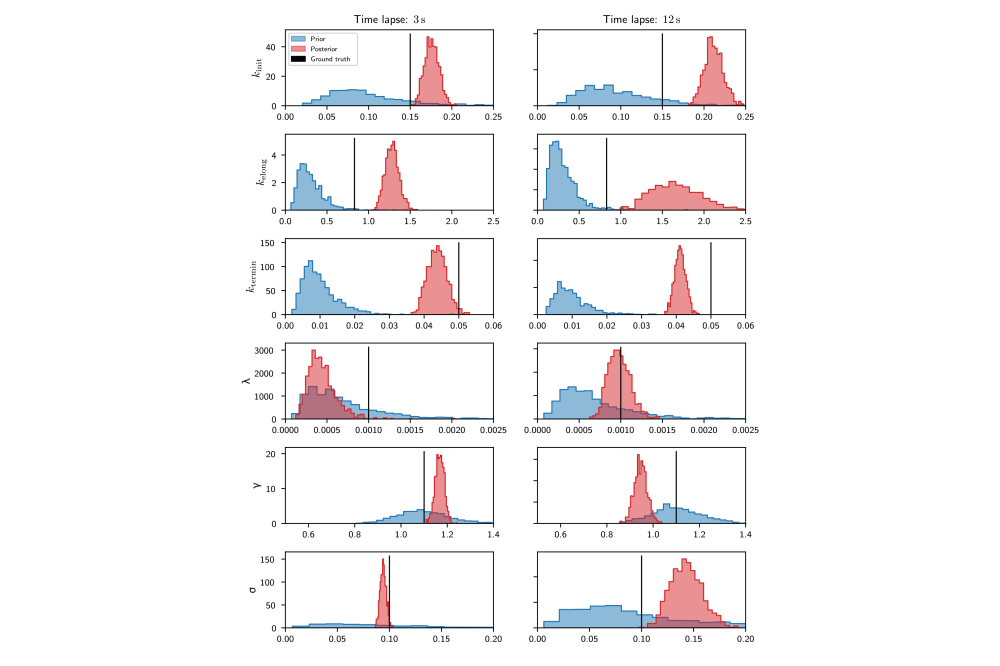
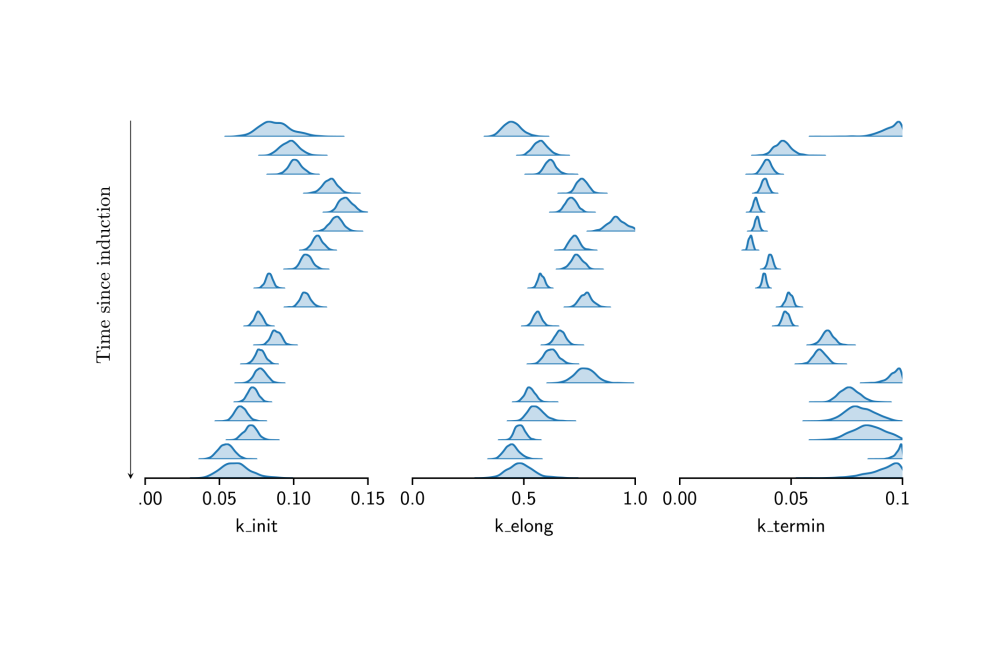
We demonstrated Hamiltonian Monte Carlo Inference on synthetic and real data. Results on the real data confirmed a time dependence of transcription parameters on the time passed since induction. However, forward simulations based on the learned parameters indicated that the model used was not able to explain the experimentally observed data. Therefore, a family of more detailed models was developed for which Hamiltionian Monte Carlo inference was too computationally expensive. Instead, a variational inference approach was used that turned out to work well.
Discussion
We have established that our approach can be applied to infer transcription parameters from experimental data showing non-stationary dynamics. For the next phase of the project, we plan a systematic evaluation and comparison of different model configurations. The goal is to identify a model that is most probable given the data without being unnecessarily complex.