Numerical Methods for the Model of Spatial Random Permutations and a Connection to Schramm-Loewner Evolution I
Introduction
We made several numerical calculations regarding the model of Spatial Random Permutations (SRP). This is a model in statistical mechanics and is of recent interest. In this model we look at random permutations of lattice points, which can also be identified as a directed Graph, where each point is connected with its target point via an arrow, such that cycles in the permutation form loops in the graph. As typical in models in statistical mechanics the probability of a certain realization depends on the energy of the system, where the energy and probability of a realization are defined in such a way that short arrows are more likely. The degree to which long arrows get penalized depends on the parameter alpha of the system.
We modify this model in the way that we force a path in the system which starts at the origin and goes to a boundary point. We believe that there is a connection between this model and the concept of Schramm-Loewner Evolution (SLE), which is a certain family of random curves in the complex half plane. The SRP model is hard to handle analytically, so we want to show some connections via numerical calculations. Because we want to look at geometrical quantities and therefore have to look at large systems to avoid finite effects, we need a lot of computation power. The main quantity we look at is the probability for a path in the SRP model to pass left to a certain point in a reasonable sense. In the case of SLE this probability is given by Cardy's formula.
Methods
We use Markov Chain Monte Carlo methods, more precisely the Metropolis Chain method, to get samples of our system and compute several quantities with that. In that sense we start with a permutation and mix it in several steps by changing the targets of some points in each step. But we change only if either the new permutation has less energy or at random, where the probability in that case depends on the energy difference. We found out that in order to get reasonable independent samples, a very high amount of mixing steps needs to be done. This is one reason why it takes high computation power to simulate this model. The code is written in C, and we use MPI to parallelize the computation of the samples. To generate the random numbers we use the Mersenne Twister (SFMT).
Results
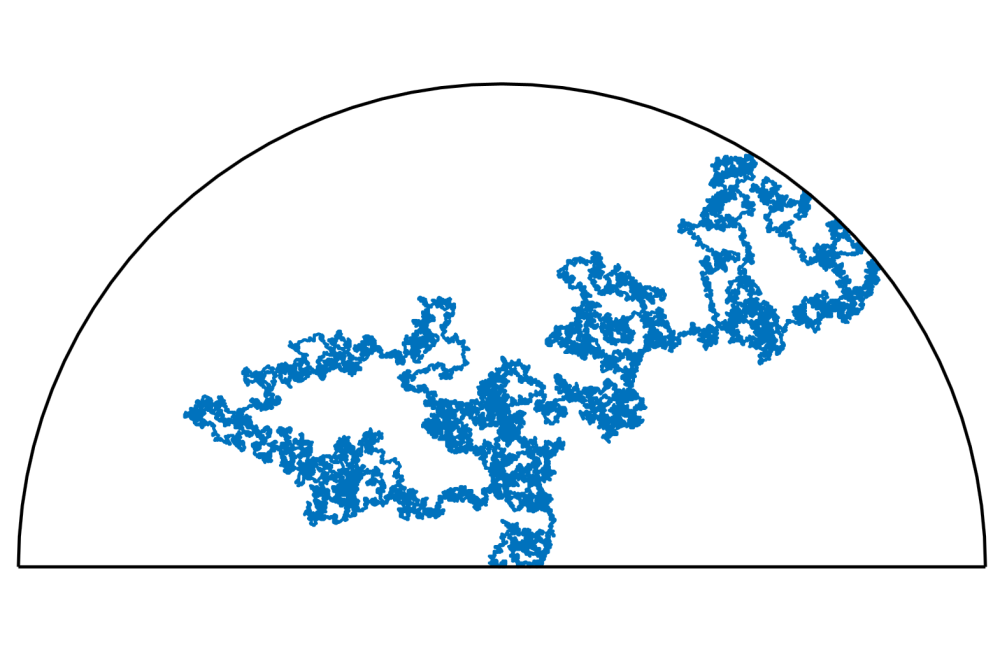
We used the main part of this period to look for the right model for simulation. There were a lot of issues to handle with regarding the right choice of lattice or the boundary conditions. At the half of the period we came to the conclusion that a lattice with a half circle boundary is appropriate for our simulations, and then we had to deal with issues regarding the construction of the path, especially how to choose the endpoint. We decided to choose the endpoint for each sample uniformly on the half circle boundary and then start the mixing with a permutation where the path ends at that point. During the mixing, we keep the endpoint fixed. This setting seems to be promising, and early computations gave results which are very similar to the ones Cardy's formula predicts.
Discussion
However, we need yet to do further calculations to get more precise results, and we need to make more statistical analysis of the results. Also we want to do calculations for other parameters of the system. Further, we want to investigate other numerical ways to hint a connection between SRP and SLE, which seem promising.