Approximately Solving Mean Field Games via Entropy-Regularized Deep Reinforcement Learning
Introduction
Reinforcement Learning (RL) has proven to be an empirically very successful approach to solving sequential decision problems. It has numerous applications today, e.g. in robotics, strategic games or communication networks. Many such applications are modeled as special cases of Markov games, which has led to empirical successes in multi-agent RL (MARL). However, MARL problems quickly become intractable for large numbers of agents and existing solutions offer few theoretical guarantees. Here, Mean Field Games (MFG) are a recently proposed, broad class of more tractable models with many homogeneous agents. As the solution of general MFGs still remains difficult, we propose an approximate solution methodology.
Methods
The framework of MFGs was first introduced in the continuous setting of stochastic differential games. In the meantime, it has sparked great interest and investigation both in the mathematical community, where interests lie in the theoretical properties of MFGs, and in the applied research communities as a framework for solving and analyzing large-scale multi-agent problems. At its core lies the idea of reducing the classical, intractable multi-agent solution concept of Nash equilibria to the interaction between a representative agent and the "mass" of infinitely many other agents - the so-called mean field. The solution to this limiting problem is the so-called mean field equilibrium (MFE), solving a forward evolution equation for the agent's masses, and a backward optimality equation of agent optimality. Importantly, the MFE constitutes an approximate Nash equilibrium in the corresponding finite agent game of sufficiently many agents, which would otherwise be intractable to compute. In high-dimensional scenarios, we apply established deep reinforcement learning methods and empirically combine fictitious play with our approximations.
Results
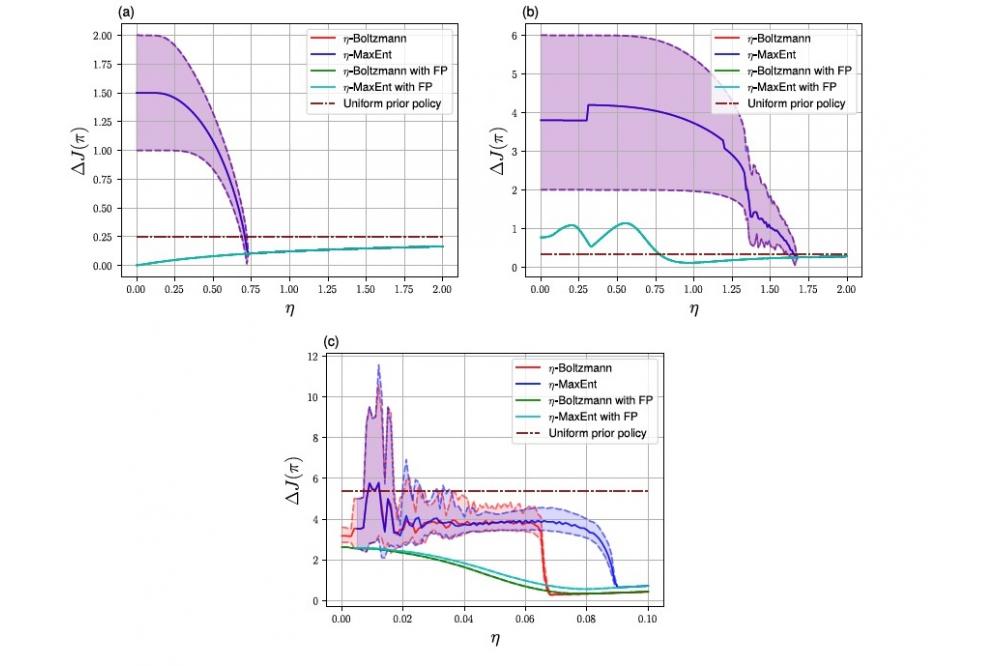
We show that many discrete-time finite MFGs are not solvable using existing methods such as fixed point iteration or fictitious play. Instead, we apply entropy regularization, weakening the requirement of optimal behavior to only near-optimal behavior. As a result, we obtain provable convergence to approximate mean-field equilibria in problems where existing methods fail. As can be seen in Figure 1, our method succeeds in finding better approximate mean field equilibria than reachable with existing approaches. The result is a computational solution to very large multiagent problems that could not be handled otherwise.
Discussion
We have shown that even finite MFGs typically cannot be solved by exact fixed point iteration or fictitious play alone. Entropy regularization in combination with deep reinforcement learning may enable feasible computation of approximate MFE. We believe that lifting the restriction of inherent contractivity is an important step in ensuring applicability of MFG models in practical problems. We hope that entropy regularization and the insight for finite MFGs can help transfer the MFG formalism from its so-far mostly theory-focused context into real world application scenarios. Nonetheless, there still remain many restrictions to the applicability of the MFG formalism.
Outlook
For future work, an efficient, automatic temperature adjustment for prior descent could be fruitful. Furthermore, it would be interesting to generalize relative entropy MFGs to infinite horizon discounted problems, continuous time, and continuous state and action spaces. Moreover, it could be of interest to investigate theoretical properties of fictitious play in finite MFGs in combination with entropy regularization. For non-Lipschitz mappings from policy to induced mean field, the proposed approach does not provide a solution. It could nonetheless be important to consider problems with threshold-type dynamics and rewards, e.g. majority vote problems. Most notably, the current formalism precludes common noise entirely. In practice, many problems will allow for some type of common observation between agents, leading to stochastic as opposed to deterministic mean fields.