DNS of Viscoelastic Fluids
Niethammer, Matthias DNS of viscoelastic fluidsFigure 1: Three-dimensional flow field of the negative wake effect behind a bubble rising in a viscoelastic fluid. The region of negative vertical flow behind the trailing end of the bubble is visualized in red.
Matthias NiethammerIntroduction
Recent numerical stabilization approaches provide new opportunities for viscoelastic flow simulations. The numerical solution of rheological constitutive equations for viscoelastic fluids is known to be prone to stability issues beyond some limiting degree of fluid elasticity, generally referred to as the “High Weissenberg Number Problem’’(HWNP). Modern numerical stabilization methods effectively alleviate the HWNP and enable stable simulations of viscoelastic flows in the technical relevant range at high degrees of fluid elasticity. The present project aims to study highly viscoelastic flows by combining numerical stabilization approaches with the Computational Fluid Dynamics (CFD) package OpenFOAM. Particular research focus is put on the direct numerical simulation of rising bubbles in a viscoelastic fluid matrix.
Methods
A generic stabilization library for viscoelastic flows is developed on top of the open source CFD software package OpenFOAM, which provides a finite volume method on general unstructured meshes [1,6]. The stabilization library is implemented by heavy use of generic C++ template metaprogramming, runtime polymorphism and overloading and it is fully parallelized, using the Message Passing Interface (MPI). For the three-dimensional direct numerical simulation of viscoelastic two-phase flows an extended algebraic volume of fluid (VoF) method is proposed in [2,6]. For the VoF method a complete set of governing equations is derived by conditional volume averaging the local instantaneous bulk equations and interface jump conditions. The homogeneous mixture model is applied for the closure of the volume-averaged equations. An additional interfacial stress term arises in this volume-averaged formulation for which a novel second-order accurate finite-volume discretization scheme is proposed in [2,6].
Results
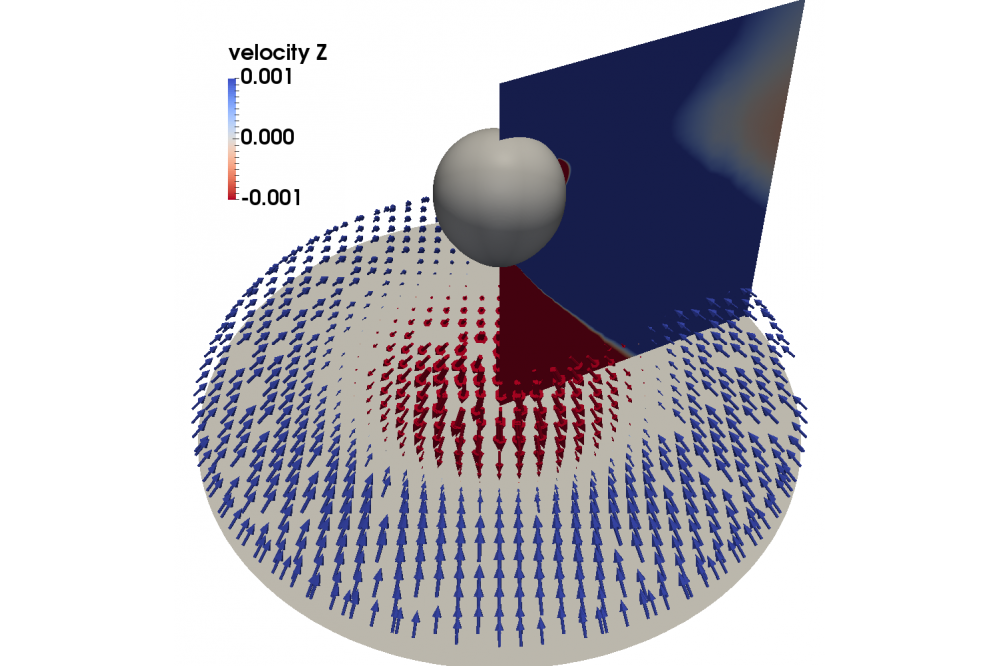
A detailed benchmark study is presented for the entry flow of an Oldroyd-B fluid in a 4:1 contraction geometry above the critical Weissenberg number [1,6]. Extensive computational resources are used to study the mesh-convergence of different stabilization methods and different constitutive models. It turns out that the applied methods are stable at high Weissenberg numbers above the critical limit and effectively alleviate the HWNP. Moreover, all methods converge towards a unique solution when the computational grid is successively refined. A novel finding is that the mesh-sensitivity depends highly on the particular representation of the constitutive equation. Our results suggest that the most accurate results are obtained with the root conformation representation when a small root function is used [1,6]. Results of the extended VoF method for single bubbles rising in a viscoelastic fluid are reported in [2,6]. The extended VoF method provides reliable predictions of characteristic viscoelastic flow phenomena, such as the velocity discontinuity (BVD) that refers to a rather abrupt increase in the steady bubble rise velocity, when their volume exceeds a critical value. The BVD is captured quantitatively correct by the extended VoF method, compared to experimental measurements [2,6]. Besides the BVD, another viscoelastic flow phenomenon, the so-called negative-wake effect, is predicted (see Figure). Additional numerical schemes are implemented to further improve the performance of the DNS. New results of the rising bubbles in a viscoelastic fluid are for the first time obtained for higher polymer concentrations. The computation of higher polymer concentrations is more challenging due to the larger fluid relaxation times, but contribute to the understanding of the physical mechanism of the BVD.
Discussion
A novel unified numerical finite volume framework for the simulation of viscoelastic flows at high Weissenberg number in complex geometries is developed and extended to two-phase flows by a VoF method. The stability issues related to the High Weissenberg Number Problem are addressed by a novel generic stabilization framework, which is coupled with the open-source CFD platform OpenFOAM. The viscoelastic flow in benchmark geometries at high Weissenberg numbers is studied, obtaining new results for highly elastic flows that were published in [1-6]. The most important findings are that the numerical methods are stable beyond the critical Weissenberg number. The mesh convergence depends on the particular representation of the constitutive equations and the results tend to be more accurate when small root functions are used instead of the logarithm conformation representation. DNS of a rising bubble in a viscoelastic fluid were performed and the capability of the extended VoF method to predict characteristic flow phenomena such as the rise velocity jump discontinuity are demonstrated. Quantitative agreement is achieved between the numerical results and experimental measurements. The numerical framework is promising for further scientific research. Further DNS of bubbles rising in a viscoelastic fluid will be studied in order to contribute to the knowledge of the physical mechanism for the BVD.
