Multiscale Modeling of the Impact of Dislocations on the Electro-Chemo-Mechanical Behavior of Lithium-Ion Battery Electrodes
Introduction
In this project, diffusion in Lithium-ion battery-electrodes is investigated on the microscale. Diffusion is often an origin for mechanical damage to LiB-electrodes, as heterogeneous ion distribution can cause large stresses in the material and finally lead to cracks and failure. Defects, in particular dislocations, can have a distinct influence on the heterogeneity of concentration fields. Dislocations are line defects with pairwise tube like compressive and tensile stress fields along the dislocation line that influence the local chemical composition by changing the local free energy due to the dislocation self stress. We study the ion redistribution around dislocations and analyse the effects on the ion mobility and driving forces.
Methods
We use a fully coupled Chemo-mechanical model within the Moose framework for the finite element method. The mechanical problem assumes linear elasticity with the displacement as in- dependent field variable and the strain and stress are calculated as auxiliary variables. The diffusion problem is solved in a mixed formulation for the concentration and the chemical potential, which reduces the integration order. The chemical potential is defined as the derivative of the free energy with respect to the concentration and is a function of the concentration and hydro- static stress field. The time evolution of the concentration is governed by the diffusion equation, which defines an ion flux proportional to the chemical potential gradient and in consequence coupled with the mechanical problem.
In the mechanical model, a concentration dependent eigenstrain is defined to resemble lattice expansion upon ion intercalation. Dislocations are implemented with a dislocation eigenstrain that resembles the dislocation induced lattice distortion calculated from a convolution of the burgers vector integrated over the dislocation glide plane, based on an analytical formulation for the dislocation. Taken together, the concentration field is sensitive to the local concentration and stresses, where the stress field itself is affected by the concentration and the presence of dislocations.
The model was expanded by calculating configurational forces based on the generalized Eshelby stress tensor to derive driving forces for dislocations interacting with the concentration field and defects as grain boundaries. Challenges for the simulation lie within the long range stress fields of dislocations, with a core of only several nm. Accordingly, a very fine mesh in a large domain is needed to achieve the necessary resolution.
Results
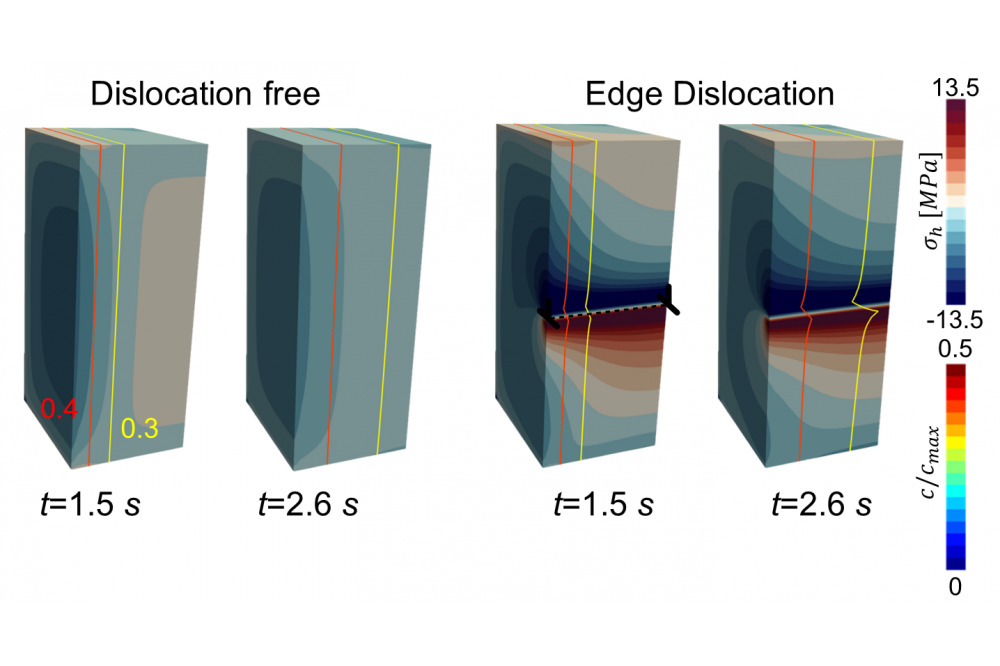
The stress field for an edge dislocation was benchmarked with the classical analytical singular solution and analytical nonsingular solutions from literature. Due to the interaction of dislocations and diffusive ions, an ion enrichment on the tensile side and depletion on the compressive side was observed, which was confirmed with a benchmark to an analytical solution.
Further, the diffusion induced stress (DIS) was reducing the dislocation stress field. The ion redistribution and DIS was observed to be strongly dependent on the state of charge of the material and asymmetric vs. the average concentration of 50 %. Explicitly, a stronger enrichment on the tensile side for low concentration and vice versa for high concentration a stronger depletion on the compressive side was found.
The maximum DIS in the tensile region of the dislocation is found at a concentration below 50 % and the maximum DIS in the compressive region is found at a concentration above 50 %. An anisotropy for the mobility around a dislocation was not found, but the mobility is concentration dependent and in accordance with above observations, dislocations induce a strong mobility heterogeneity.