Gravity-Wave Breaking
Gravity-Wave BreakingFigure: Temporal evolution of the cross-section of total buoyancy (colors) from 3D a direct numerical simulation of a breaking inertia-gravity wave. Yellow contours show an isosurface of the Q-criterion representing intense turbulent activity [5].
Introduction
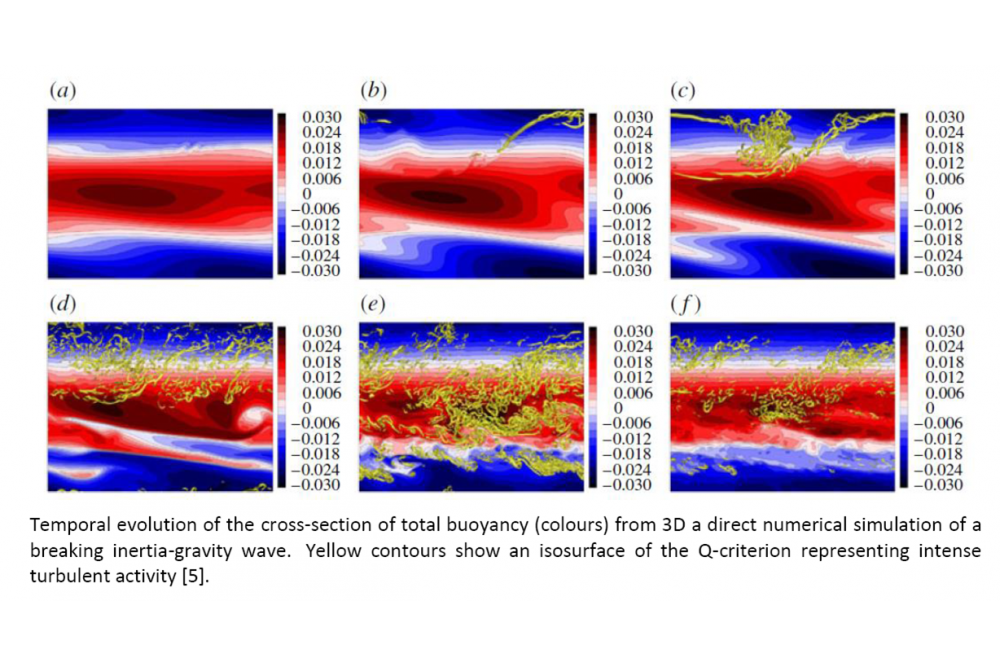
The explicit examination of the smallest scales of atmosphere and ocean dynamics is the subject of research on the dynamics of breaking inertia-gravity waves (GWs). One motivation for this work is the important role of gravity-wave breaking in the middle atmosphere. Via this process and the ensuing acceleration or deceleration of the middle-atmosphere circulation gravity waves play a decisive role in middle-atmosphere dynamics. Incorporation of the latter into climate models, however, is crucial for correct simulations of our climate variability on decadal and longer time scales. Moreover, gravity waves also form an essential direct connection between the smallest-scale turbulence and the synoptic (daily-weather) scales in the troposphere. There are indications that future progress in weather prediction and climate modelling will depend crucially on a better understanding of the corresponding processes. Also in the oceanic context gravity waves are thought to be a key element in the generation of turbulence. The latter is vital for a mixing which is sufficiently strong so as to keep the thermohaline circulation in motion.
Methods
GWs being too small in scale to be explicitly resolvable in weather and climate models, their effect must be parameterized by corresponding modules. These parameterizations should be tested against simulations that can accommodate both the propagation of the waves (requiring domains of tens to hundreds of kilometres in all three spatial dimensions) and their breaking (requiring resolutions of between centimetres and a few metres, depending on the altitude). Only large-eddy simulation (LES) is suited for this task. On the other hand, since LES treats the small-scale turbulence by parameterizing the sub-gridscale (SGS) physics, it also needs to be validated against turbulence-resolving direct numerical simulation (DNS). Recent work [1,5,2] has provided fully resolved direct numerical simulations of breaking monochromatic inertia-gravity waves under conditions appropriate to the upper mesosphere. Several test cases were considered, each exhibiting turbulence with varying degrees of intensity and intermittency in time and space. These direct numerical simulations have then been used as reference cases for testing two largeddy simulation schemes: the dynamic Smagorinsky method and the implicit Adaptive Local Deconvolution Method (ALDM) [3], originally developed for modelling isotropic incompressible turbulence but adapted for use with stratified turbulence [4], as it occurs in the atmosphere. The schemes have been compared in terms of how well they reproduce the decay of the wave and the energy dissipation as functions of time during the breaking process, with results varying considerably with the type of wave-breaking event considered. For a case involving strong turbulence ALDM turns out to be the better choice, while for cases with weak turbulence and a partially laminar flow field the dynamic Smagorinsky method has advantages6.
