Fast Circularisation of Rydberg Atoms
Introduction
Circular Rydberg states refer to the valence electron of a highly excited atom in a circular orbit. Due to their very long lifetime, they are an ideal tool in quantum technology. For example, they can be used in the field of quantum sensing where quantum systems are used to measure physical quantities, like electric or magnetic field strengths, with a higher sensitivity than classically possible. However, due to the fragility of quantum states, these measurements have to be performed as fast as possible to avoid loss of information due to the detrimental interaction of the system with its environment. In our work, we aim to prepare circular states of Rydberg atoms as fast and accurate as possible to enable protocols for high precision measurements.
Methods
We are using quantum optimal control theory (OCT) to shape radio frequency pulses in order to drive the system fast and efficiently from the known initial state towards the target state – the circular state. To this end, we optimise the shape of an initial guess pulse numerically until we reach the target state with the desired fidelity. First, we perform the optimisation while taking experimental restrictions on pulse amplitude and bandwidth into account, and second, we aim to find the shortest possible time to perform this task, called the quantum speed limit, when lifting the experimental limitations. This can be done by performing the optimisation for several hundreds of guess pulses with decreasing length to find the shortest pulse which still accomplishes the task.
Results
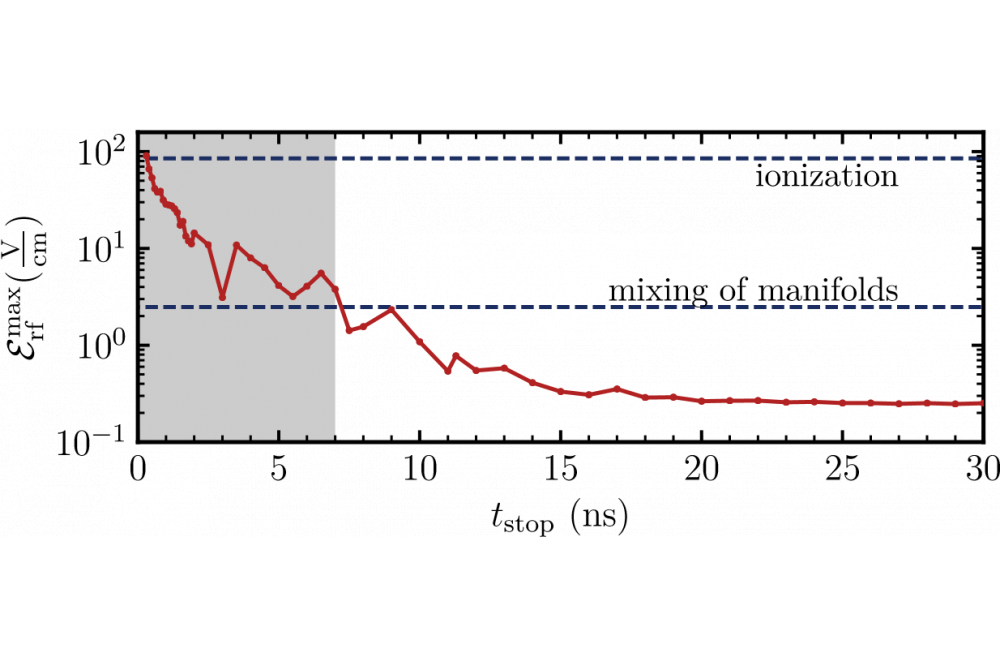
We find optimised pulses which drive the Rydberg atom efficiently to the circular state under given experimental conditions in a two-step approach. When the dynamics of the atom are visualised on the so-called Bloch sphere, the initial state is represented by a ring around the south pole (Fig. 1 left-most panels) while the target state is a Gaussian centred at the north pole (right-most plot in the lower panel). The solution for an efficient circularisation is to first transform the ring into a Gaussian-shaped state (panels at 20 ns) and then to perform a rotation towards the north pole. When looking for the quantum speed limit we find that the circularisation is in principle possible until the theoretical model breaks down (Fig. 2). For an efficient numerical calculation it was necessary to perform a few approximations like restricting the subspace of the system. When the duration of the circularisation is decreased, this results in an increase of the required field strength. Eventually, the strong driving field leads to a strong deformation of the energy level structure and the approximations break down. Beyond this border, we cannot make further conclusions about the ability to perform the circularisation.
Discussion
The achieved results permit to perform the circularisation of Rydberg atoms in a short time with a high fidelity under experimentally feasible conditions. Theoretically, the task can be performed very fast and the required time for the protocol is mainly limited by the amplitude of the radio frequency pulse available in the experiment. The circularisation time and fidelity are limiting factors for high precision measurements of magnetic and electric field strengths and hence, the improved protocol will allow for higher sensitivities in parameter estimation using circular Rydberg atoms.
Outlook
The optimised pulses can be implemented in the experiment using an arbitrary waveform generator. Moreover, the method of OCT can be utilised to achieve further, more sophisticated optimisation goals like the preparation of a superpositions in the Rydberg manifold.