Numerical Simulation and Optimization of Acoustics of Flight Turbine
Introduction
The increase of the aerodynamic noise produced in turbulent flow is recognized as a factor that impairs the humans‘ health. Therefore, the simulation and the optimization of the acoustics in the turbulent context has become increasingly significant in the engineering field. The acoustic simulation is performed in two steps. First, the acoustic source is obtained by solving the turbulent flow field. Second, starting from the acoustic sources, the acoustic quantities are calculated by solving the Linearized Euler Equation (LEE).[1] The Direct Numerical Simulation (DNS) and the Large Eddy Simulation (LES) can be used to simulate the turbulent flow. The drawback of both methods is that they are expensive in terms of the computational cost. Particularly the DNS is only applicable to very simple geometry. The Reynolds Averaged Navier-Stokes (RANS) method, which reduces the computational cost largely, is unfortunately not adequate for the simulation in this case, because exactly the perturbations, which are averaged in RANS, is relevant for the acoustic source.
Methods
The hybrid methods, which combine the LES and the RANS methods, are considered to be a promising compromises in terms of the computational cost and the accuracy. Therefore, the hybrid methods are applied in the simulation of flow of the acoustic problems. In the present work, the investigation focuses on two points. First, it is to investigate, weather the hybrid model, the Detached Eddy Simulation (DES), can provide an acoustic source with sufficient accuracy. For this purpose, the acoustic sources and the acoustic quantities are to be compared with the results calculated using DNS or LES. The DES has been implemented and verified. The acoustic quantities obtained by means of DES needs to be verified with the help of appropriate test cases. Second, the optimization of the acoustics is also to be conducted using the sensitivity method. The sensitivity method is a gradient-based method, which is an relatively efficient strategy of optimization in comparison with the gradient-free method.[2]
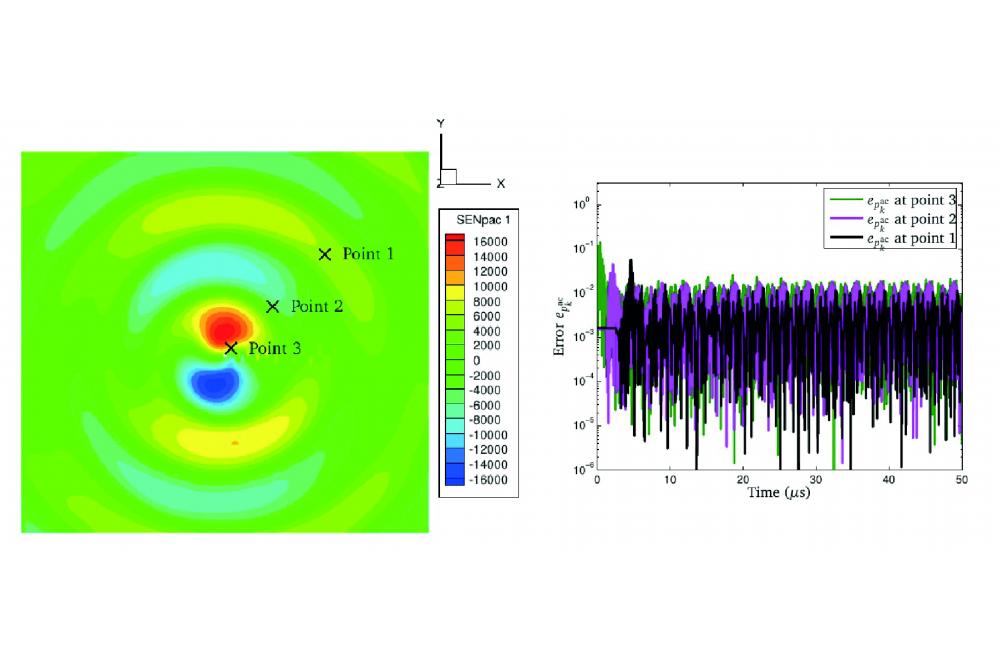
The major difficulty is the calculation of the sensitivities of the acoustic quantities with respect to the design variables, which are the parameters that can be changed to achieve the optimization. The key point here is to verify, weather the sensitivities have sufficient accuracies. The acoustic sensitivity solver for the laminar flow has been already implemented and verified with the help of a cylinder flow (Fig.1), which used 8 cores for the computation of the flow and 8 cores for the sensitivities, while the computation between the flow and sensitivity solvers are realized through MPI.[3] The sensitivities are compared with the finite differences, which can represent the gradient with sufficient accuracy.
Results
Fig.1 shows that the errors of the sensitivities of acoustic pressure solved using the implemented solver have relative errors of approximately 0.01, which is quite acceptable. The performance of the sensitivities in the turbulent flow needs to be further investigated. It can be infered that the computation demand for the acoustics and acoustic sensitivities in the turbulent flow will be larger than the ones in the laminar flow. The high-performance computer can drastically reduce the computation time by distributing the computation onto more cores, and it can therefore enormously facillitate the research.