Thermal Transport Properties in Magnetic Tunnel Junctions
Thermal Transport PropertiesFig. 1: Sketch of the MTJ. The barrier (3 monolayers MgO) is sandwiched by two ferromagnetic layers (FexCo1-x) and connected to semi-infinite Cu leads, which are in the bcc-Fe structure. One ferromagnetic layer is the fixed layer (10 monolayers), whereas the other is the free layer (5 monolayers). The relavite angle between the two magnetizations ML and MR of the two layers is given by Θ. The torque acting on the magnetization of the free layer can be decomposed into an in-plane and out-of-plane component.
Introduction
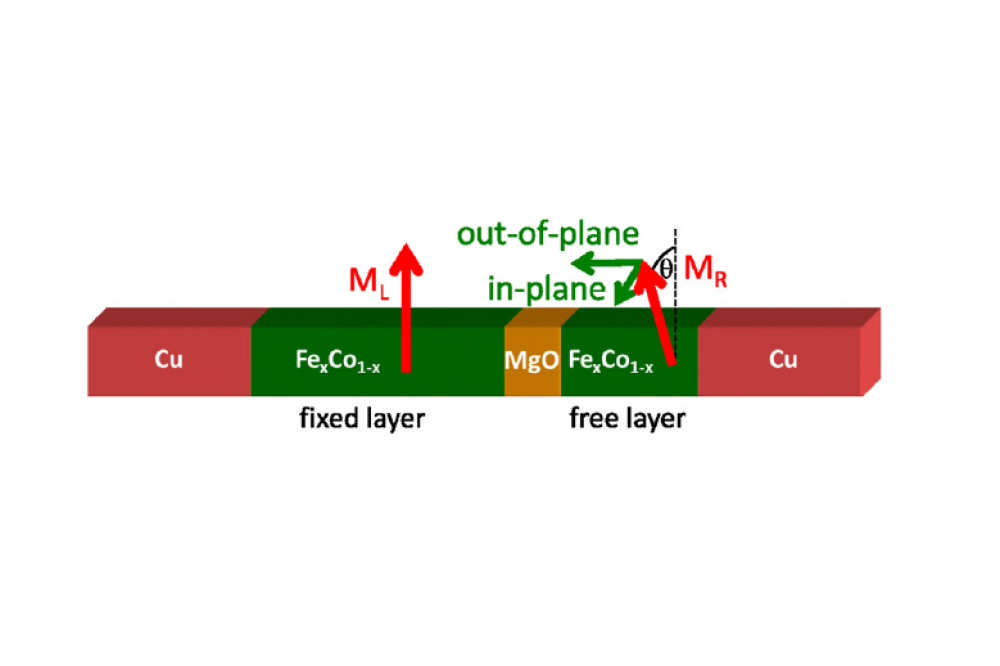
The new research field of spincaloritronics is the combination of two research fields: magnetism (spintronics) and thermoelectrics. In the field of spintronics, magnetic tunnel junctions (MTJs) are already used in applications such as read heads in hard disks and storage elements in magnetic random access memories. The tunneling magneto resistance effect (TMR) is exploited in both applications. A MTJ consists of a barrier sandwiched between two ferromagnetic layers, a free layer, and a fixed layer (Fig. 1).[8]
Methods
Our research group predicted theoretically[1] that the Seebeck effect (the creation of an electric field by a temperature gradient in a material) changes with a change of the magnetic orientation of the ferromagnetic leads relative to each other, similar to the tunneling magnetoresistance effect (TMR). Our prediction to this tunneling magneto-Seebeck (TMS) effect was confirmed experimentally.[2] Furthermore we investigated the role of the interface termination[3] and of the ferromagnetic lead material[5] on the TMS and the angular dependence of the TMS,[7] which were confirmed experimentally.[2,7,9] While the TMS is the influence of the spin-dependent transport properties (TMR) on the thermoelectric properties (Seebeck), one can also consider the reversed case. In this way the thermoelectric effect influences the spintronic properties. This effect is called thermal spin-transfer torque (TSTT), where the idea is that the free layer can be switched just by applying a temperature gradient without any bias voltage.
Results
We showed with our calculations that the TSTT in MgObased MTJs is much smaller than the bias driven ones and therefore large temperature gradients are needed.[8] For this reason very thin barriers (3 monolayers) are required to achieve thermal switching. We showed that one can optimize the TSTT by tuning the material decomposition of the ferromagnetic leads.[4] For all calculations we used our own code by means of a full-relativistic Korringa-Kohn-Rostoker Greensfunction method (KKR) which can handle non-collinear magnetism. Additionally the code is extended to describe alloys and can calculate several transport properties such as transmission, spin-transfer-torque and magneto-Seebeck. The required vertex corrections for the calculation of the transport properties for alloys are implemented as well.[6]
