HKHLR - HPC Hessen

Analysis of the Lyapunov Stability of Grid Forming Converters Using Sum of Squares Optimization

Analysis of the Lyapunov Stability of Grid Forming Converters Using Sum of Squares Optimization

Siyuan Li_Analysis of the Lyapunov stability of grid forming converters using sum of squares optimization_Figure1 Siyuan Li_Analysis of the Lyapunov stability of grid forming converters using sum of squares optimization_Figure1

Figure 1: Contour of Lyapunov function(colour), the domain D (red), the ROA (black) and the gradients (arrows)

Siyuan Li_Analysis of the Lyapunov stability of grid forming converters using sum of squares optimization_Figure2 Siyuan Li_Analysis of the Lyapunov stability of grid forming converters using sum of squares optimization_Figure2Figure 2: Comparison of the radius for domain D β (solid) and the value of ROA c (dash) with different parameter values of kd .
Siyuan Li_Analysis of the Lyapunov stability of grid forming converters using sum of squares optimization_Figure3 Siyuan Li_Analysis of the Lyapunov stability of grid forming converters using sum of squares optimization_Figure3

Figure 3: Size of ROA with respect to voltage and current controller parameters

Introduction

With the increasing integration of renewable energy sources, modern power systems are shifting from conventional networks dominated by large synchronous generators to the converter-dominated networks. This shift significantly reduces the inertia of the system which helps resist disturbances during the operation, and results in larger transients. To maintain stability in the converter-dominated, low-inertia systems, nonlinear analysis methods are required. One of such approaches is Lyapunov stability analysis, which can evaluate whether a system will return to equilibrium after being disturbed. However, applying this method to high-order systems involves high complexity numerical calculation and optimization problems that demand substantial computational power. This project leverages High-Performance Computing (HPC) to enable these demanding calculations. The study focuses on a simplified system consisting of a grid-forming converter connected to an external grid, aiming to determine its stability boundaries under various operating conditions and find the optimal parameters for the control system of the converter.

Methods

This project consists of two phases, firstly calculation of the Region of Attraction (ROA). Using Sum of Squares (SOS) optimization, the Lyapunov function is derived to estimate the ROA. It describes a domain, from which the system states will in certain circumstances return to a stable operation point. Secondly, controller parameter optimization In the second phase, Particle Swarm Optimization (PSO) is employed to automatically tune the converter’s control parameters. The algorithm iteratively searches for parameter combinations that maximize the ROA, using its projection size on specific space state plane as the optimization criterion.

Results

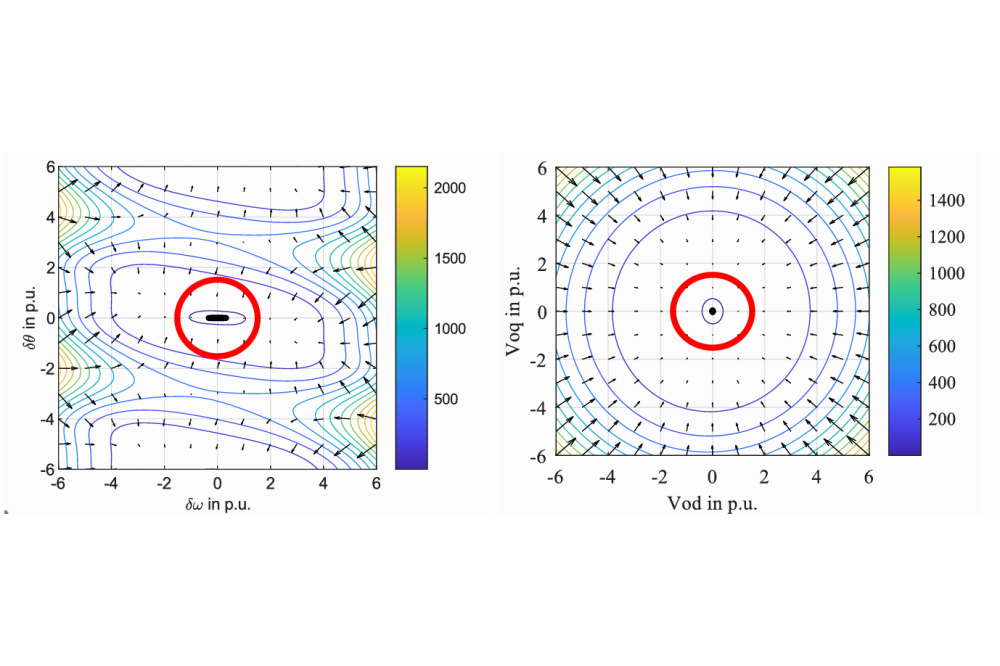
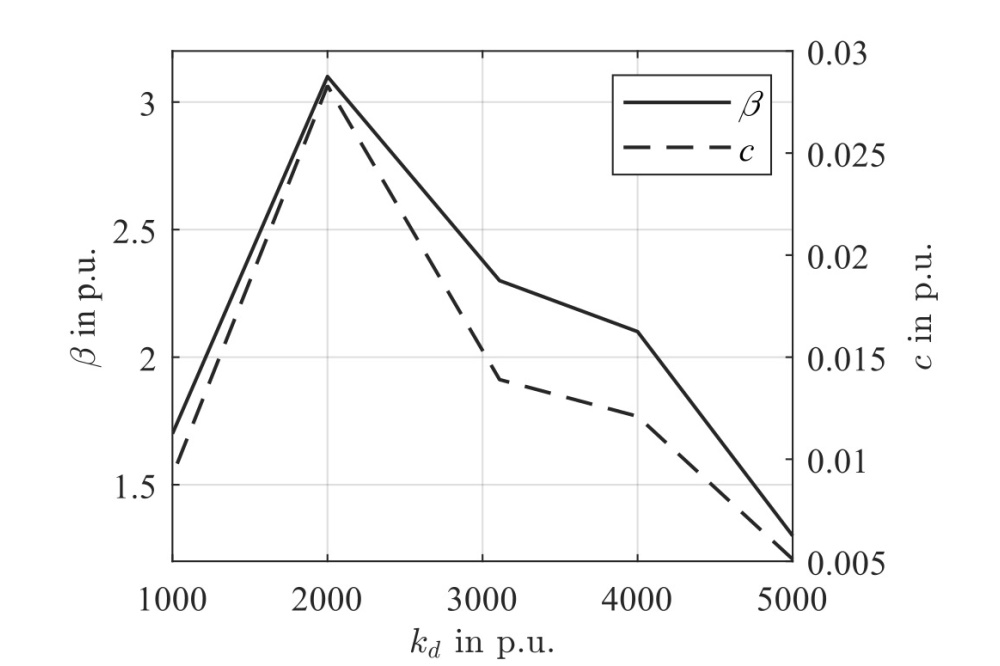
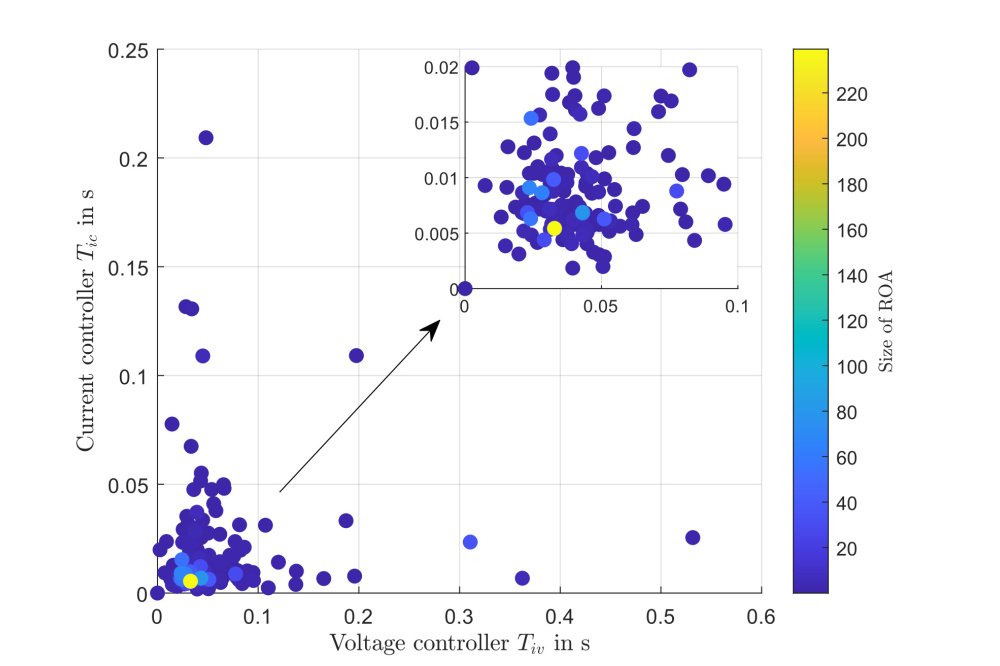
Figure 1 illustrates the derived contour of the Lyapunov function of the grid-forming converter, projected onto two-dimensional planes to visualize its dynamic behaviour, which is calculated by the SOS optimization. Furthermore, the influence of the damping factor of the grid forming converter kd on the ROA is investigated. The change of the stability region β and ROA c with the damping factor kd are illustrated in Figure 2. Based on the Lyapunov stability analysis method, the PSO algorithm is implemented to search for the optimal controller parameters for the grid-forming converter. The results are shown in Figure 3, which is illustrated by the relationship between size of ROA and the time constants of converter controllers. After optimization, the voltage and current controller time constants are adjusted from Tiv = 22.21 ms, Tic= 31.83 ms for the original parameters to Tiv = 32.77 ms, Tic = 5.42 ms. This adjustment significantly improves the converter’s dynamic response, and the ROA increased from 1.02 to 239.21.

Discussion

The Lyapunov function in Figure 1 confirms that the system is asymptotically stable, aligning with conventional small-signal stability results. However, the computed ROA is conservative, underestimating the actual stability region. The analysis of the damping factor kd in Figure 2 shows: as kd changes, the ROA increases at first and decreases after a certain point, revealing a local optimum between kd=1000 and kd=3110. After applying the tuning method, the time constant of the current controller is significantly reduced, suggesting a noticeable change in the current response to be observed in the simulation results. The size of ROA increases from 1.02 to 239.21, indicating a substantial improvement in stability performance under disturbances. Future work will explore hybrid optimization strategies that combine the global search capabilities of PSO with local refinement techniques, enabling faster convergence. Additionally, the approach will be extended to multi-objective problems, considering different types of disturbances and system configurations, including multi-converter and large-scale networks.

Last Update

  • Last Update:

Participating Universities