First-Principles Calculations of Spectroscopic Signatures II
Introduction
Linking experimental and theoretical observations on a physical system is one of the key objectives of modern science. The task of our group is to calculate spectroscopic signatures of solids and molecules from first principles, i.e. solely using the basic laws of physics and without employing empirical parameters. The calculated electronic and optical properties give direct access to observable spectra, which can be compared with experimental measurements. This allows us to explain the microscopic physical mechanisms in the considered systems and to verify proposed physical models. Yet, modelling the macroscopic properties of a given material on the basis of its atomic structure is a challenging task, which is carried out in two steps. Firstly, the electronic ground state of the system is modelled in the framework of the density functional theory (DFT). Structural and electronic excitations can be calculated in a second step. We calculate spectroscopic signatures of different systems, ranging from 0D clusters to 3D bulk materials. The strong connection with an experimental counterpart allows us to develop a combined approach which goes beyond state-of-the-art investigations. Thus, we establish novel and powerful tools, which support the knowledge gain in materials science.
Methods
The density functional theory (DFT) permits the computation of the electronic ground-state energy and the ground-state charge density of a given atomic configuration (solids and molecules). These quantities result from the Kohn-Sham (KS) eigenvalue equations, which are solved within the following selfconsistent scheme: Calculated from a test charge density, the effective potential is inserted into the KS equations, which are then solved by matrix diagonalisation. The eigensolutions determine a new charge density, which yields the new test charge density for iterating the procedure. The iteration stops if the total energy changes less than a threshold of choice. The number of required iterations can considerably be reduced by sophisticated guesses for the initial charge. The KS equations are solved with efficient and established numerical algorithms. The periodic unit cell approach discretises the differential operators into matrices acting on the Fourier coefficients of the wavefunctions (plane waves). The infinite sums are truncated according to the convergence of macroscopic quantities (usually the total energy). The continuous Brillouin zone is integrated on a grid of k-point samples. The number of k-points is reduced by symmetry relations and typically amounts to ∼100 for bulk systems, and ∼10 for surfaces. Similarly to the number of plane waves, the optimal number of k-points is determined by the convergence of macroscopic quantities. The matrices are diagonalised within efficient iteration schemes, most importantly the Davidson block diagonalisation and a residual minimization scheme (direct inversion in the iterative subspace, RMM-DIIS).
Results
Subproject A s devoted to the investigation of the LiNbO3-LiTaO3 solid solutions, mostly simulated by DFT as implemented in the VASP and QuantumEspresso codes. The approach to the calculation of the nonlinear optical response based on the calculation of the polarization in the time-domain, which we implemented during the runtime of the project, has been applied to LiNbO3 and LiTaO3, revealing the origin of the strong nonlinear optical coefficients measured in the experiments. The heat capacity of the same materials has been furthermore calculated from first principles, considering both the ferro- and paraelectric phases. We have simulated the ferroelectric domain walls in LiNbO3 and LiTaO3 crystals as strained material. This is a simplified model suggested by the X-ray investigation of the domain walls.
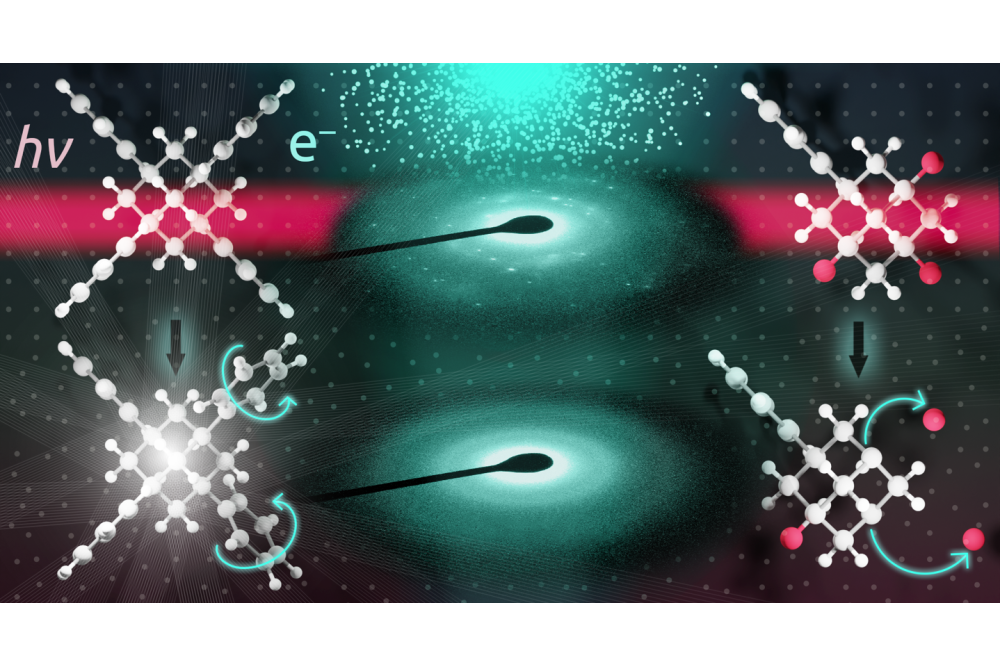
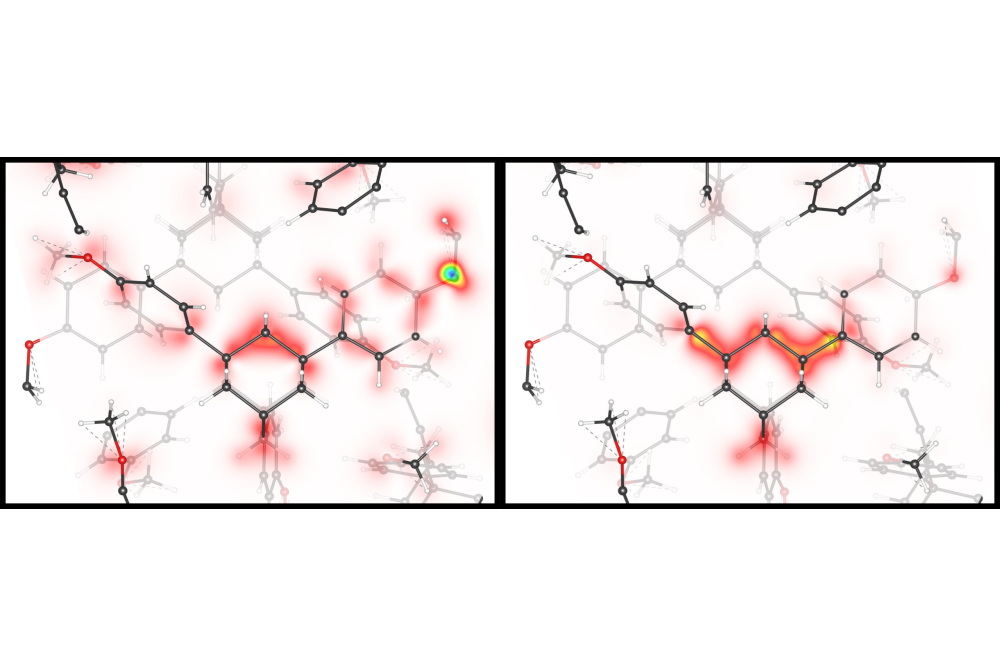
Subproject B is dedicated to the investigation of the adamantane-based molecular clusters and their unique optical properties as investigated in the research group FOR2824. Prototypical model systems are the adamantane shaped [(RT)4R6] clusters (with R = organic group; T = C, Si, Ge, Sn; E = O, S, Se, Te, NH, CH2, ON•). After calculating the ground state atomic and electronic structure of different molecules, we have explored the effect of chemical modifications (ligand field) and habitus (single molecular cluster, molecular crystals) on the optical response. In a further collaboration with Prof. D. Mollenhauer (Justus-Liebig-University of Gießen), we investigated dimers, trimers and tetramers of the optically nonlinear clusters.
Discussion
Subproject A: The heat capacity of the materials has been compared with corresponding experimental results from the group of Prof. S. Ganschow at the IKZ in Berlin, showing an excellent agreement and providing further insight towards the materials properties undergoing a structural phase transition. Our calculations on the strained cells were performed in the framework of a cooperation with Prof. Lukas Eng (Technische Universität Dresden), and might be used to calibrate the signal of Raman spectroscopy and to explain the lattice dynamics of uniaxially strained samples in a natural way. Similarly, the reduced formation energy of several lattice defects in strained samples explains the defect accumulation at the domain walls.
Subproject B: On the basis of our calculations, we could demonstrate white light generation from clusters which form glasses, which represents a breakthrough toward a possible application of these materials. Understanding the interaction of the cluster dimers allows an initial assessment of the interactions in the materials. The investigation indeed allows to roughly predict the habitus of the molecular compounds on the basis of simple rules, which is of crucial relevance, as only amorphous materials lead to white light generation. Our calculations explain the results of the experimental investigation of this class of molecules, synthetized by our experimental colleagues (Prof. S. Dehnen at the KIT and Prof. P. W. Schreiner at the Justus-Liebig-Universität Gießen) and characterized by optical measurements within the group of Prof. K. Volz at the Philipps Universität Marburg.