Cold Quantum Gases in two Dimensions with IM-SRG and FCI
Fabian Brauneis_Cold Quantum Gases in two Dimensions with IM-SRG and FCI_Figure1Figure 1: Left panel: Energy of 3 spin-up and 3 spin-down fermions in a two-dimensional harmonic trap interacting attractively. Calculations were performed with the FCI and the IM-SRG method. Both methods agree well for weak interactions while for stronger interactions the methods deviate. For even stronger ones IM-SRG calculations diverge. Also shown is the position of the Higgsminimum which signals the beginning of the experimentally interesting parameter regime.
Right panel: Energy of 4 bosons in a two-dimensional harmonic trap interacting attractively plotted over the two-body energy for different single-body basis cutoffs (maxenergy). For strong interactions, no convergence can be achieved. This area is the one where the universal aspects of the bound state appear. For larger particle numbers, the convergence worsens.
Introduction
Ultracold atomic gases allow for a high control over experimental parameters such as the particle number or the dimensionality. This motivates theoretical studies on lower dimensional systems which behave quite different from the usual three dimensional world we live in. It also motivates the study of few-to-many-body transitions: How do many-body phenomena emerge from the underlying few particle physics? How many particles are needed to observe many-body aspects? In recent years, experiments with fermions in two dimensions gained a high control over the particle number and interaction. These experiments showed e.g. the precursor of a many-body effect (Higgs-mode) and its transition to the many-body limit by starting from just two fermions and increasing them to up to twelve. However, on the theoretical side, simulations of these experimental setups have only been performed for up to six particles due to numerical limitations. We plan to extend these studies using a different numerical method (see below) which allows to speed up computation by parallelization. These calculations also require large amounts of memory, demanding the use of HPC. Furthermore, we plan to investigate bosons in two dimensions interacting via short range interactions. Theoretical works based on mean-field arguments postulated universal behavior of the particles: an exponential scaling of the radius and energy with an increasing particle number. We want to test if these properties are visible in an experimental setting and therefore perform ab initio calculations for such systems. Due to the exponential increase of the energy and shrinking of the radius, such calculations need a very large configuration space making their computations impossible on regular machines.
Methods
We use the flow equation method (also called in-medium similarity renormalization group method [IM-SRG]) to perform our simulations. This method has been used with great success in nuclear physics. We used this method in the past for one-dimensional systems of cold bosons and extend it now to higher-dimensional systems. The flow equation method maps a reference state onto the ground state of the system. To be able to go to large particle numbers, this transformation is not done exactly, some parts of it are truncated. These truncated parts are small if the reference state is a good guess. In this case, the method works well and ground state properties can be calculated. However, if the overlap between the reference state and the true ground state is too small, the method fails and produces large errors or even diverges. To check the validity of the method, we test the flow equation method with the full-configuration interaction method (FCI), which diagonalizes the Hamiltonian matrix of the system in a finite configuration space. Note that this method only works well for small particles numbers due to a rapidly increasing configuration space for larger ones.
Results
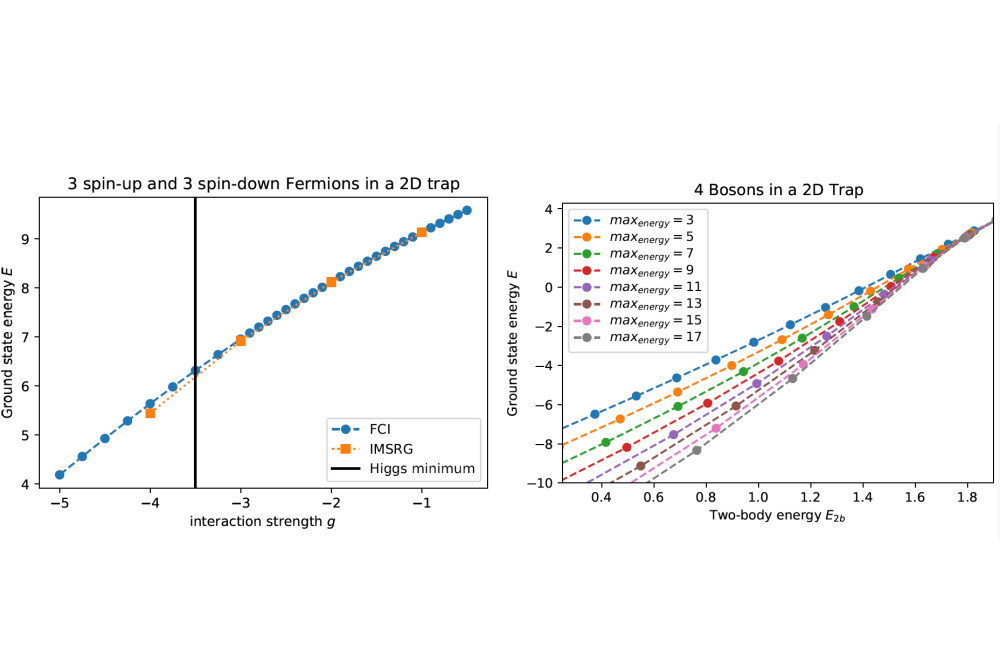
For the two-dimensional fermions we find that the flow equation method is only in good agreement with the FCI in a limited parameter regime. For weak interactions, both methods agree well, however, for stronger interactions the chosen reference state is not good enough and the results start to disagree. For even stronger interactions, the flow equation method even starts to diverge. See for example Fig. 1 left panel where we show the ground state energy for 3 spin-up and 3 spindown fermions as a function of their interaction strength. For the two-dimensional bosons, we find that the needed configuration space to observe the universal behavior of the 2D bosons is too large even on a HPC. Our data points show no sign of convergence with an increasing configuration space. We show an example of this in Fig. 1 right panel where one can see that for stronger attraction between the bosons (smaller two-body energy), the data points do not converge with increasing single-body basis cutoff. This parameter regime is the one where we expect universal behavior to emerge.
Discussion
Unfortunately, the parameter regime of stronger interactions is the experimentally interesting one where effects like the precursor of a Higgs-mode are observed. Since the flow equations show a good agreement for weak interaction but not for a strong one, we need to improve the reference state of the system for these cases. Currently, we use a formulation of the flow equation method where a single Slater determinant is used as a reference state. However, the physics of the true ground state of the system consist of highly correlated fermions making a mapping impossible. Instead a more sophisticated reference state needs to be used. For the two dimensional bosons the problem of non-convergence even on HPC suggests that a straightforward ab initio simulation of universal two-dimensional bound states might not be possible. Instead, we need to tailor the numerics specifically for this system. We are currently working on implementing a new basis which takes into account the knowledge of previous mean-field studies. With this improvement we expect convergence in significantly reduced configuration space.
