Improved Nuclear Energy-Density Functionals from Local Chiral-Effective-Field-Theory Interactions
Introduction
Nuclear energy density functionals successfully reproduce properties of nuclei across almost the entire nuclear chart. However, nearly all available functionals are phenomenological in nature and lack a rigorous connection to systematically improvable nuclear forces. This issue might be solved with an energy density functional obtained from first principles. As an intermediate step towards this goal we construct the GUDE family of functionals that is obtained from a hybrid scheme consisting of contributions derived from chiral effective field theory and a phenomenological Skyrme part. Both the functional optimization and the calculation of properties of several hundred nuclei are computationally heavy tasks, which require the use of high-performance computing facilities.
Methods
The functionals are constructed from long-range pion-exchange contributions derived from chiral effective field theory at the Hartree-Fock level amended with a phenomenological Skyrme part. The direct pion contributions are included in a quasi-exact fashion by approximating the pion-exchange potentials by sums of Gaussians. The exchange terms are treated with a density-matrix expansion. The Skyrme part of the functionals involves 14 optimization parameters. They are determined by fitting to experimental data from finite nuclei. The data set includes ground-state energies, odd-even mass differences, charge radii, and fission isomer excitation energies. The optimization is carried out using the POUNDERS algorithm. The functionals are employed to calculate nuclear properties using the Hartree-Fock-Bogoliubov method.
Results
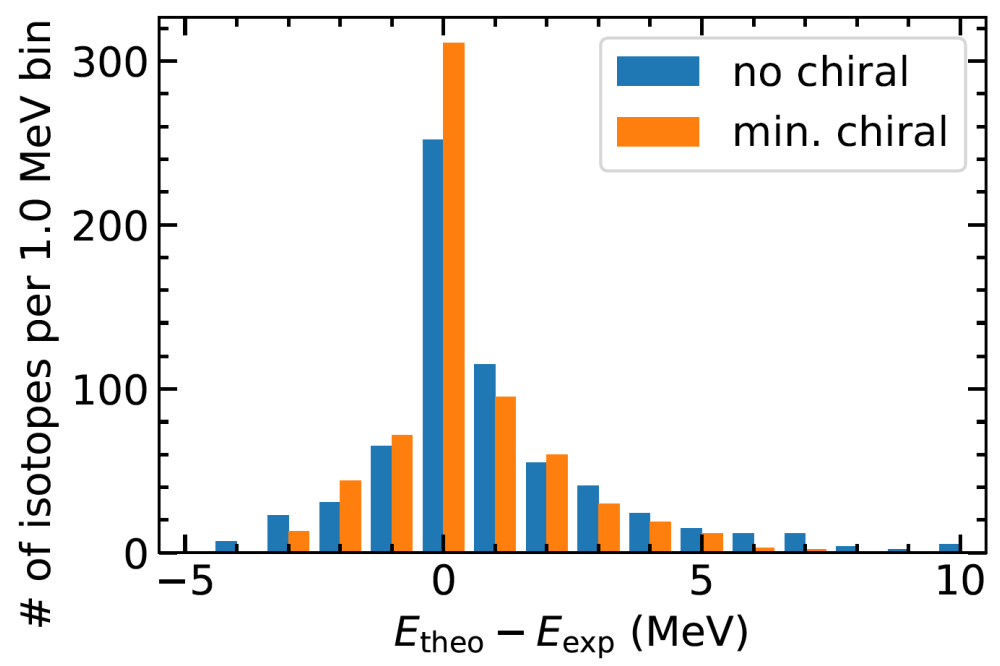
When including pion contributions at leading or next-to-leading order in the chiral expansion, we find no improvements over a reference Skyrme functional constructed following the same protocol. Also, the inclusion of terms arising from three-nucleon seems to have no effect. However, when considering pion exchanges between two nucleons beyond next-to-leading order in the chiral expansion, we find significant improvements. In particular, the accuracy of describing nuclear ground-state energies is improved: the global root-mean-square deviation to experiment is reduced by about 30%. The figure shows a histogram of the differences between predicted and experimentally measured energies for the reference functional (“no chiral”) and a functional with chiral terms beyond next-to-leading order (“min. chiral”). Other investigated observables of finite nuclei are not strongly influenced by the inclusion of pions. Some properties of infinite nuclear matter, for instance, the nuclear incompressibility and the slope parameter, change significantly when including pions beyond next-to-leading order.
Discussion
We analyze the importance of different pion contributions and identify which terms drive the observed improvements. We find that attractive direct pion contributions at next-to-next-to-leading order and some leading-order exchange terms are relevant. Since pions are incorporated without adding further optimization parameters to the functionals, the improvements can be attributed to the functional form of these terms. This suggests that such terms will be relevant when generating an energy density functional completely from first principles. In the future, the isovector part of the functionals, which is relevant for extreme neutron-rich conditions in astrophysics, should be constrained better. The determination of correlated uncertainties for the fit parameters is also of interest.