Effect of Infinite Time-Horizons on Genetic Algorithms
Introduction
Genetic Algorithms (GAs) are a popular heuristic optimization method inspired by biological evolution. We implemented a GA that incorporates ideas from Tabu Search, another optimization heuristic. It saves all visited solutions in a special data structure called a Bloom filter and then avoids them in future generations. Finding the ground states of Ising spin glasses was used as a test problem. First simple runs showed promising results, and we therefore wanted to analyze in greater detail how much better it performs in comparison to a traditional GA and what parameters produce the best results.
Methods
In a traditional GA a population of individuals, each representing a solution to a specified problem, is evolved through mutation and recombination. To solve the optimization problem, each solution gets assigned a fitness value and only the individuals with the highest fitness get carried over to the next generation.
The algorithm implemented by us inserts the individuals of each generation into a Bloom filter. Before adding a selected individual to the next generation it checks whether it is in the filter and discards it if that is the case. Bloom filters are a probabilistic data structure, that can efficiently store a large amount of elements. It is then possible to query whether an element was previously inserted, but because of its probabilistic nature a probability of false positive results remains.
A spin glass is a disordered magnetic system. Minimizing the energy of a simplification of such a system called an Ising spin glass is an easy to implement but sufficiently hard to solve problem. Test runs of our GA on Ising spin glasses showed good results which is why we decided to analyze it further using a larger amount of runs.
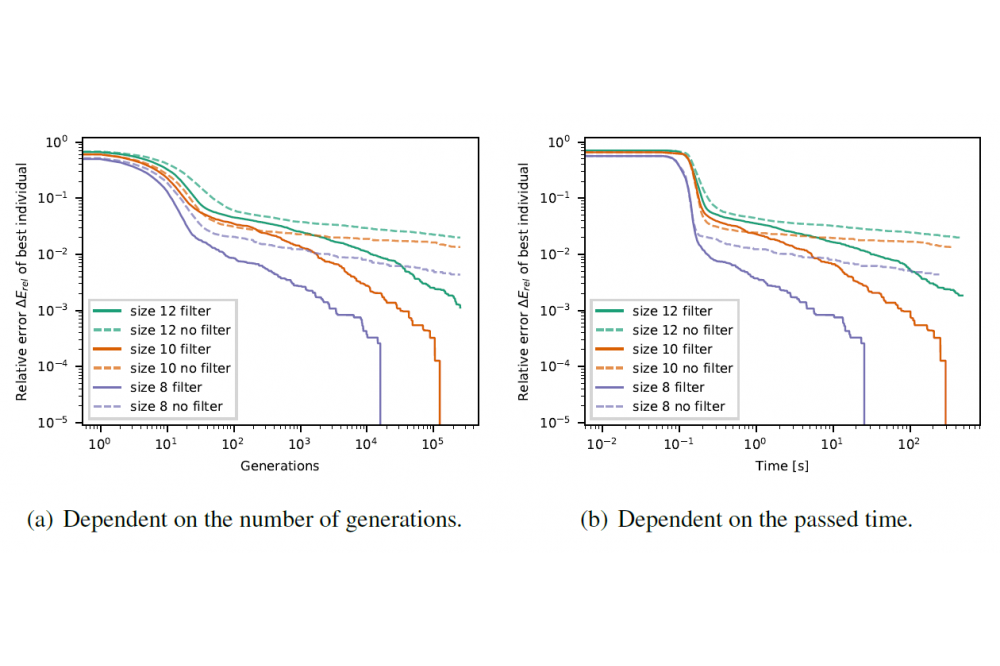
A parameter scan was performed on the HPC. Multiple parameters like the mutation rate and the recombination rate, as well as two newly introduced parameters, that control the filter mechanism, were varied. For each configuration 100 runs with different spin glass instances and random generator seeds were executed. 2D Spin glasses with periodic boundaries and normal distributed interactions were used. Scans using instances with side length 8, 10 and 12 were performed. In total more than 2 million runs were started, each on a single core and independent of the others. MPI was merely used to distribute the configurations.
Results
As can be seen in Fig. 1 the hybrid GA finds the ground states of Ising spin glasses on average in fewer generations and in less time. An analysis of all runs showed that the implemented GA needs more time to calculate a single generation but still finds the ground states more often and in less time than a traditional GA with the same time limit. For spin glasses of size 12x12 the best configuration without filter found the ground state in 5 out of 100 runs while the best configuration with Bloom filter found it in 81 out of 100 runs.
The superior performance could only be observed when almost every individual is checked by the Bloom filter. But surprisingly it was sufficient to only insert a small percentage of each generation into the filter. The best configurations had a mutation rate below 0.7. The recombination rate had almost no effect on the performance. If the false positive rate of the Bloom filter gets too high, because too many individuals were inserted, the GA will essentially be stuck, because no individual passes the check by the filter.
Discussion
The results show that the implemented method can outperform a traditional GA if the parameters are chosen right. It will be interesting to see how well this method performs on different optimization problems like for example the Traveling Salesman Problem and if the optimal parameters are the same as with Ising spin glasses. A comparison to proven methods for each problem would be insightful as well.