Matrix Elements of New Families of Chiral Interactions
Matrix Elements of New Families of Chiral Interactions1Figure 1: Ground-state energies and radii of selected medium mass nuclei calculated with the SMS NN interaction supplemented with 3N interactions with Λ=500 MeV cutoff differing by regularization scheme. The different symbols indicate the cD-values of the 3N interaction. The results without initial 3N interaction are indicated with open black circles and the experimental values are indicated with black bars.
Thomas Hüther
Matrix Elements of New Families of Chiral Interactions2Figure 2: The low-energy constants cD and cE of the nonlocal 3N interaction at N3LO withcutoff 500 MeV optimized for the ground-state energy of 3H (blue), the ground-state energy of 4He (red), and the rms relative deviation of the ground-state energies from 3H and 4He experiments equal to 0.010 and 0.015 (green areas) and the optimum (green dot). The blue crossand the red square indicate the cD-cE pairs that also reproduce the 16O ground-state energy.
Thomas HütherIntroduction
The goal of ab initio nuclear structure theory is the description of nuclei from first principles without uncontrolled approximations, allowing calculations with excellent predictive power. All of these calculations require the construction of nuclear interactions, which is done using chiral effective field theory (chiral EFT), a framework that has been extremely successful in recent years. Using these interactions directly in a many-body calculation is computationally expensive, hence, we use the Similarity Renormalization Group (SRG) to ’soften’ these interactions. The SRG improves the convergence behavior of many-body calculations, however, the SRG itself involves large-scale numerical calculations. This project provides the next generation of chiral interactions suitable for ab initio many-body calculations.
Methods
Our main method is the SRG, which is a continuous unitary transformation of the Hamiltonian. This transformation can be written in a flow equation, that translates into a set of coupled nonlinear first-order differential equations. These are solved numerically with highly specialised codes developed within our group. The SRG decouples high- and low-momentum states and thereby prediagonalizes the Hamiltonian, which reduces the model space necessary to converge subsequent many-body calculations.
Results
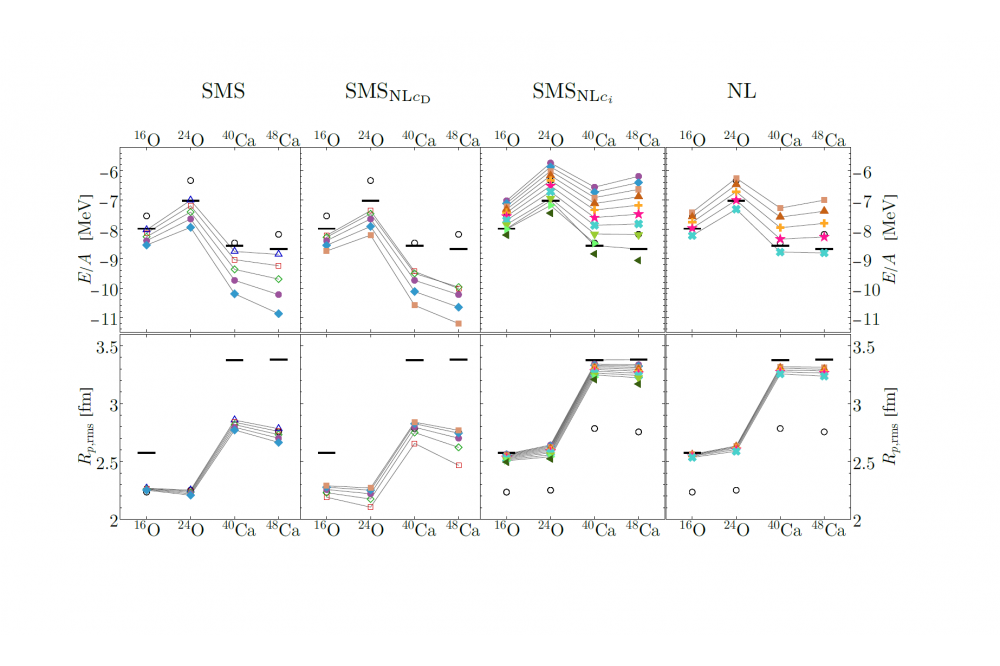
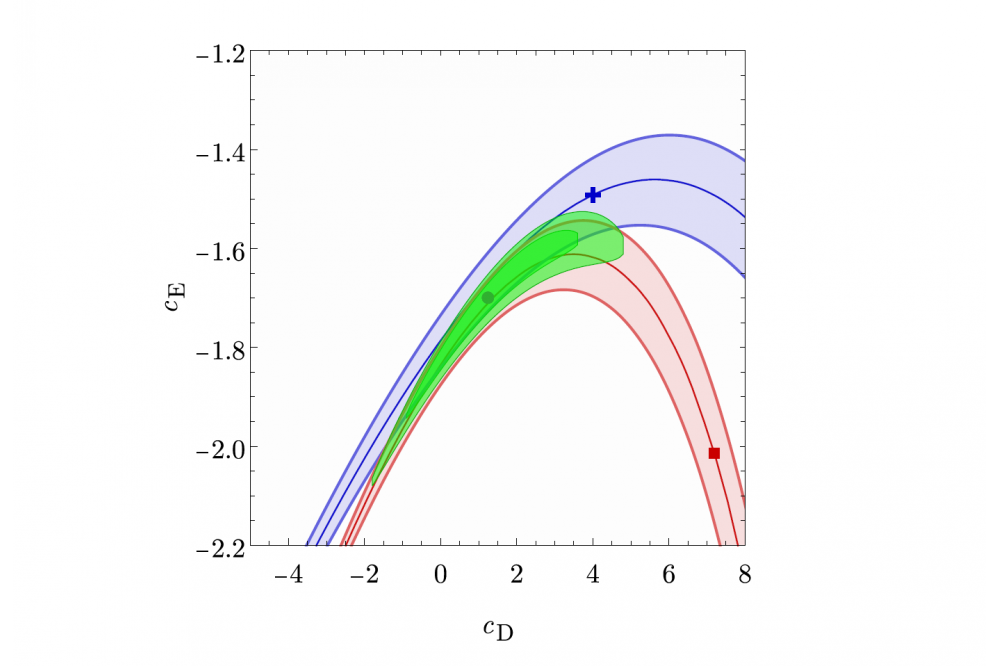
In this project we have calculated matrix elements of the next generation of chiral interactions, which we developed within the Low Energy Nuclear Physics International Collaboration (LENPIC) as well as in collaboration with Machleidt. These matrix elements have been used in many large-scale calculations within our group or by our collaborators. Furthermore, we optimized the phenomenological Gaussian four-body interaction and adapted it for tetraneutron calculations.
Discussion
The systematic order-by-order analysis of the convergence of the chiral EFT expansion and the comparison of different regularization schemes are essential for a quantification of theory uncertainties for nuclear structure observables. With the newest generation of the Entem-Machleidt- Nosyk nucleon-nucleon interaction family in combination with three-nucleon interactions developed in this project, we have an interaction that can provide reliable nuclear observables up into the medium-mass regime.
First discrepancies between theory and experiment have been found in selected open-shell nuclei in the medium mass regime. In the next project period we want to tackle these discrepancies by incorporating the SRG into the fitting procedure, which should enable the construction of even softer interactions.
Furthermore, the consistent SRG evolution of the hyperon-nucleon-nucleon interaction will be performed. Moreover, the development of the interaction family within LENPIC indicates that we are missing crucial contributions either in the interaction or in the radius operator itself. In ongoing work, we will address both higher-order terms of the interaction and the radius operator.
