Topological Susceptibility at High Temperatures from Lattice Quantum Chromodynamics
Introduction
The theory of the strong interaction, Quantum Chromodynamics, is known to have complicated topological structures called instantons, which are important for several applications. We investigated how the prevalence of topology decreases with increasing temperature, in a regime where conventional methods fail because topology becomes exceptionally rare. We developed two new techniques within a numerical approach called lattice Quantum Chromodynamics, one of which proved more effective, and we demonstrated them on a slightly simplified version of Quantum Chromodynamics called Pure-Glue Quantum Chromodynamics.
Methods
When topology becomes rare, standard Markov chain Monte-Carlo sampling is no longer effective because it simply never samples the rare topology-containing configurations. Starting from a standard code package for the implementation of lattice Quantum Chromodynamics, we developed two approaches to overcoming this problem. In one approach, we modify the Monte-Carlo weighting to enhance topological and “pretopological” configurations, enhancing the sampling (multiple topologies at a fixed temperature). The key advance in the first funding period was a method for better identifying the configurations which lie between non-topological and fully topological fields within lattice Quantum Chromodynamics, which allowed us to reweight so as to prefer these configurations and enhance the rate that the Markov chain moves between topologies. In the other approach, one compares topologies at one temperature, and then compares across temperatures separately within configurations of a fixed topology. By exploring how differently topological and non-topological configurations react to varying temperature, one can then determine the temperature dependence of topology (multiple temperatures at fixed topology).
Results
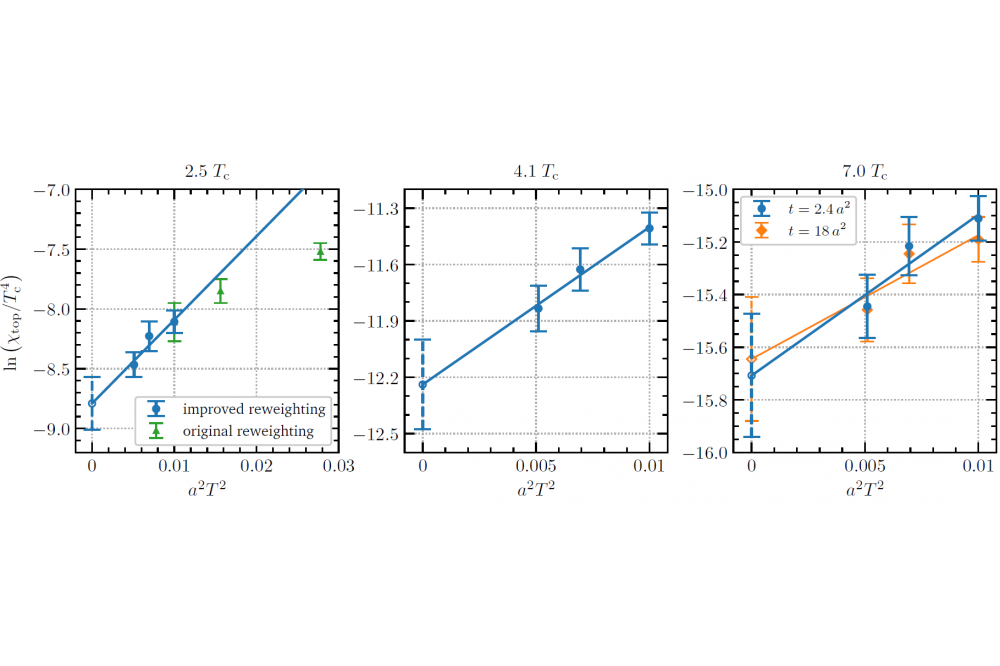
In our first approach, we used the provided computational resources to carry out a study at multiple lattice spacings and temperatures, allowing a continuum extrapolation to physical Quantum Chromodynamics, but still with a simplifying approximation (quenched). Our results, illustrated in Figure 2, were released in a preprint which is currently under peer review.
In the second approach, we were able to show that there are fundamental limitations on the method’s efficiency which render it uncompetitive with the first method. We are preparing a preprint presenting these results, but because the method is not competitive we did not attempt a continuum limit and we cut the numerical exploration short.
Discussion
Our work established the best approach for studying topology and topological susceptibility within Quantum Chromodynamics. It remains to relax the approximation (quenching) in which the effects of fermions are neglected. Unfortunately the inclusion of fermions makes several aspects of the analysis more complex and will increase the numerical costs by over an order of magnitude. Therefore the gains in statistical power we have demonstrated will be essential in achieving results in full quantum chromodynamics.