Calculating Temperature Dependent Properties of 2D Magnets
Calculating temperature dependent properties of 2D magnetsFigure 1: Calculated temperature dependent domain wall configuration in Nd2Fe14B.
Min YiIntroduction
Predicting the temperature dependent properties of magnetic materials is still challenging, which cannot be dealt with first-principle calculations and micromagnetic simulations alone. A multiscale scheme combining first-principles calculations, atomistic spin model simulations, and micromagnetic simulations should be utilized. The computation is across scale and is thus extremely expensive, requiring the computation source from high-performance computer (HPC).
Methods
We use a multiscale scheme which combines zero-K first-principles calculations, atomistic spin model simulations, and micromagnetic simulations.
Results
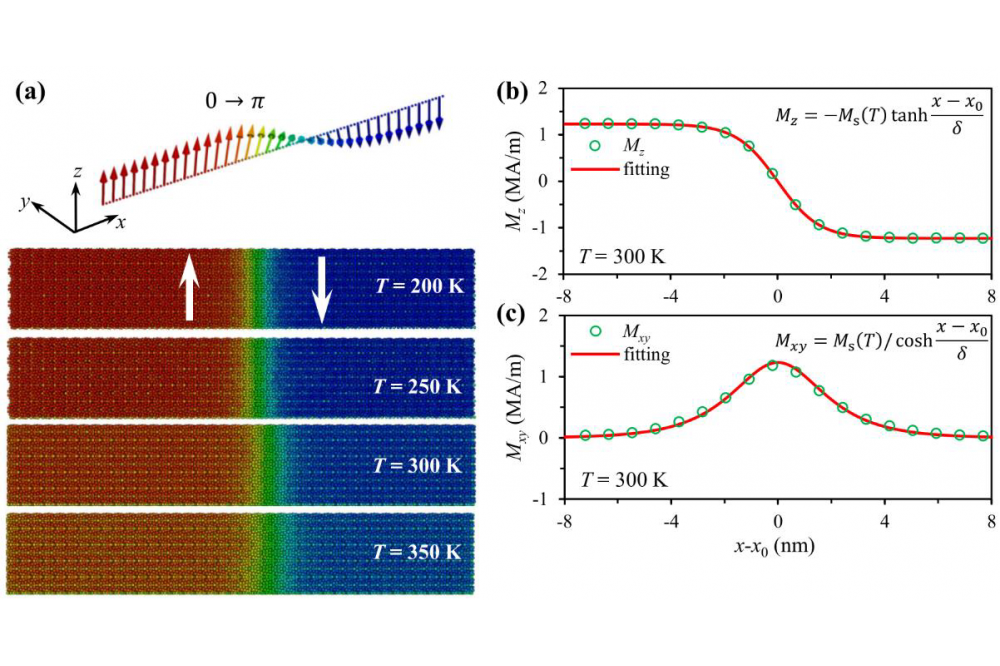
- We have predicted the temperature-dependent intrinsic magnetic properties of Nd2Fe14B by multiscale simulation integrating ab initio calculations and atomistic spin model simulations.
- We have calculated the high-temperature magnetic properties of Nd-Fe-B permanent magnets with the consideration of microstructures by multiscale simulation integrating ab initio calculations, atomistic spin model simulations, and micromagnetic simulations.
- We have applied the temperature-dependent micromagnetic simulations combining phenomenological state of equation for the calculation of magnetocaloric effect in Co2B magnetic materials.
Discussion
Temperature-dependent magnetic properties of Nd2Fe14B permanent magnets, i.e., saturation magnetization Ms(T), effective magnetic anisotropy constants Keffi(T) (i = 1, 2, 3), domain-wall width δw(T), and exchange stiffness constant Ae(T), are calculated by using ab initio informed atomistic spin model simulations. This work provokes a scale bridge between ab initio calculations and temperature- dependent micromagnetic simulations of Nd-Fe-B permanent magnets.
A computational scheme integrating the atomistic spin model (ASM) and micromagnetic simulations is proposed to predict the coercivity of Nd-Fe-B permanent magnets at high temperatures. With the ASM results as input, finite-temperature micromagnetic simulations based on the stochastic Landau-Lifshitz-Gilbert equation are performed to calculate the magnetic reversal and coercivity (Hc) at high temperatures.
We propose a calculation scheme which integrates micromagnetic simulations and the Arrott–Noakes equation for the investigation of the influence of microstructure and magnetocrystalline anisotropy on the magnetocaloric effect (MCE) in second-order magnetic phase transition materials. More extensive calculations with more complex microstructures, including different grain sizes, shapes, and orientations as well as different grain boundary properties have to be performed to gain further insight on the relation between microstructure and MCE.
