Electrical Conductivity and Relaxation via Colored Noise in a Hadronic Gas
Electrical conductivity and relaxation via colored noise in a hadronic gasFigure 1: Left: Electric current as a function of the time in Boxes of different volumes. Right: Comparison of the electrical conductivity of a pion box to an analytical calculation as a function of the temperature.
Jan HammelmannIntroduction
Calculating transport properties such as the electrical conductivity of a strongly interacting hadron gas is a difficult task, since the underlying fundamental theory (QCD) is not analytically accessible with the usual techniques. To circumvent this problem, we make use of a newly developed transport code SMASH (Simulating Many Accelerated Strongly-interacting Hadrons), which effectively solves the relativistic Boltzmann equation with realistic interactions between the hadrons. These interactions are implemented such that the cross-section between the hadrons matches with experimental measurements. Usually SMASH is used to simulate heavy-ion collisions at intermediate collision energies.
Methods
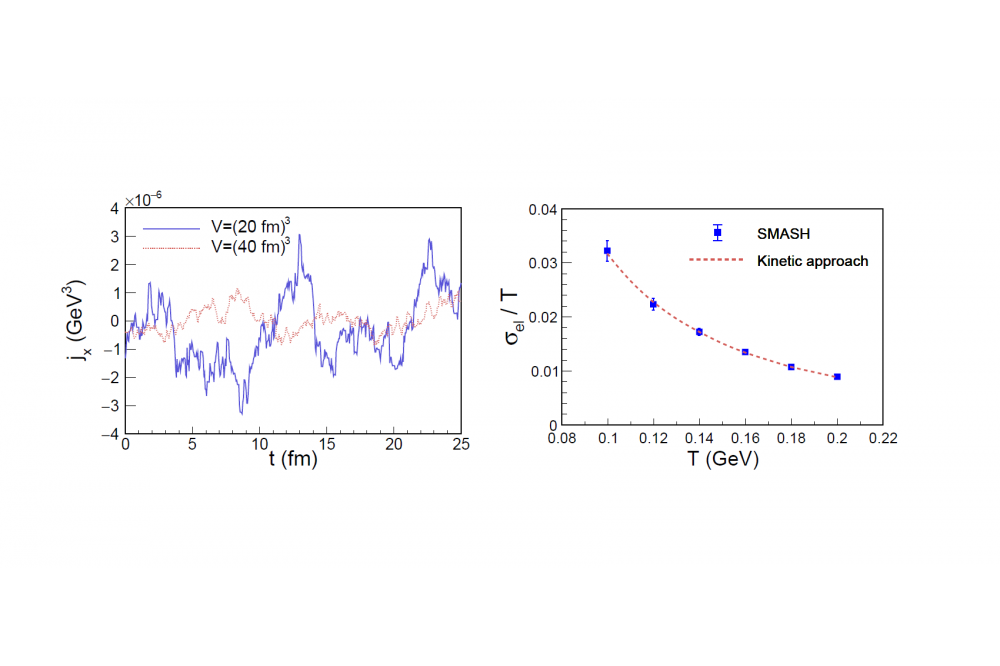
The electrical conductivity is calculated in an infinite matter system, which means to put hadrons in a box with periodic boundary conditions and let the system evolve over time. We make use of the so called Green-Kubo formalism, which relates transport coefficients such as conductivities or viscosities, to a corresponding underlying equilibrium fluctuation. In our case, we calculate correlations of the electric charge current with itself over a long period of time in an equilibrated system. From this resulting correlation function, it is possible to extract the relaxation time of the hadronic medium. The relaxation time describes a time which the system needs to relax from a non-equilibrium state to a equilibrium. Together with the corresponding temperature and volume of the box, one can calculate the electrical conductivity of the system.
Results
As a start, we begin with a comparison of our model with a well known formula for the electrical conductivity for a very simplistic system in order to ensure that our methodology is working. From this point on, we increase the number of particle species and interaction between the individual hadrons and compare our result again to an analytic calculation of a similar physical system. Especially the impact of the resonance lifetime on the transport coefficient is investigated, since it has been shown in previous works, that this can give a non-negligible contribution to the transport coefficients of hadronic matter. From this point on we further increase the number of species and interaction to our final result. We also looked at the impact of a non-zero baryochemical potential on this particular setup.
Discussion
Our results for the simple systems suggest that out methodology is stable and we can extract the electric conductivity from our model, since our results are in very good agreement with analytic calculations. In contrast to other transport coefficients, we find a very small impact of the resonance lifetime on the electric conductivity. Also for our final setup of particles, the baryochemical potential seems to have a minor impact on the final result.
Outlook
There are improvements to our calculation. First we can still increase the number of hadrons and interactions to our calculation and go to the full hadron gas as could be provided by SMASH. In addition, by increasing the number of states, baryons will contribute much more to the electric current. As a last point, it could be interesting to investigate the impact of medium modified interactions.
