High Throughput Screening of Topological Properties in Ferromagnets
Samathrakis_Ilias_High throughput screening of topological properties in ferromagnets_Figure1Figure 1: The automated MLWFs construction scheme
Hongbin Zhang
Samathrakis_Ilias_High throughput screening of topological properties in ferromagnets_Figure2Figure 2: The x-component of the anomalous Hall conductivity as a fuction of the x-component of the anomalous Nernst conductivity for several ferromagnetic compounds (left). The anomalous Hall conductivity as a function of energy for CoSe2 (right).
Hongbin ZhangIntroduction
In this work, we performed first-principles calculations to evaluate the anomalous Hall conductivity as well as the anomalous Nernst conductivity in ferromagnetic compounds. This is achieved by using an in-house developed high-throughput scheme to construct the Wannier functions automatically. Our results signify a success ratio of 89% in the construction of the wannier functions and several compounds with interesting AHC and ANC values. Specifically, the calculated AHC exceeds 2000 S/cm in PtNi3 and in addition giant ANC which can be further tuned to realize heat rectification was observed in CoSe2. Detailed analysis on the symmetry and the electronic structure was performed in order to understand the origin of such abnormal AHC and ANC.
Methods
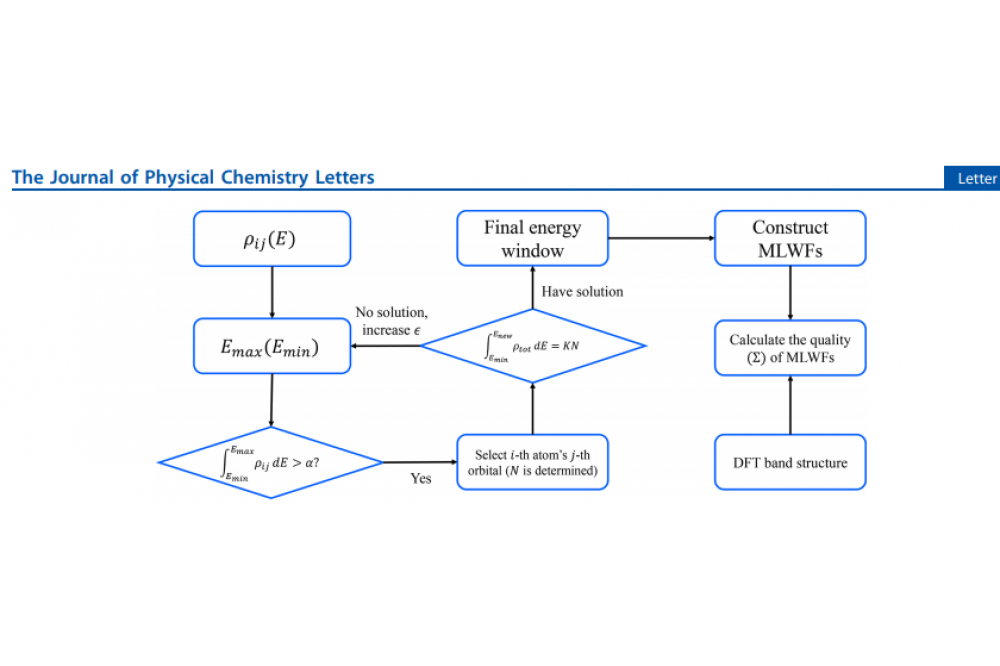
We successfully created an automatic scheme to calculate the anomalous Hall conductivity, linking VASP, Wannier90 and Wanniertools. Our DFT calculations were performed in VASP package using the projector augmented wave method. The exchange correlation functional was formulated in the generalized gradient approximation as parameterized by Perdew-Burke-Ernzerhof. The scheme was followed to project the obtained DFT Bloch wave functions onto ‘maximally localised Wannier functions’ (MLWF) using Wannier90. The input files were automatically generated using the ‘automated MLWFs construction’ scheme, illustrated in Figure 1.
Results
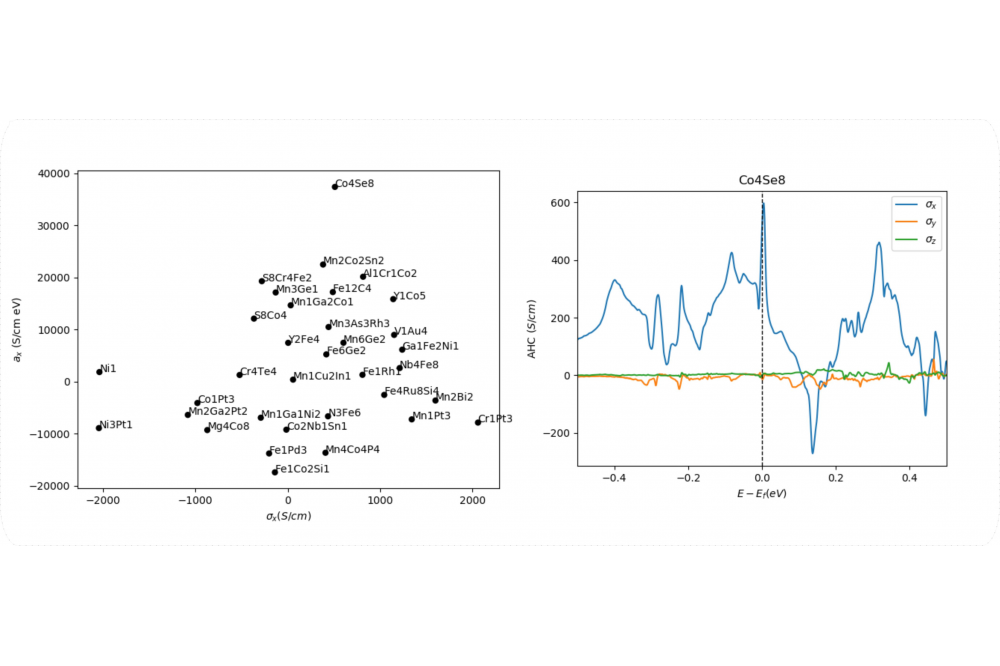
Surprisingly large AHC and ANC values are calculated in several compounds. The fully automated wannier function construction scheme was used to calculate the AHC and ANC for several ferromagnetic compounds. Interestingly, the absolute value of AHC for several compounds ranges between 1000 S/cm and 2000 S/cm, with the two largest calculated values being equal to 2060 S/cm and 2044 S/cm and being attributed to CrPt3 and PtNi3 respectively. It is noted the our values are larger than the largest reported value of approximately 1250 S/cm, calculated for FeSn film in Ref. [10]. As for the ANC, the calculated value for CoSe2 reaches 37351 S/(eV·cm) and is the largest among all the others. Additionally, the AHC versus energy curve of CoSe2 exhibits a spike, located 4meV above the Fermi level and the possibility of tuning the Fermi level precisely at the positions of the spike can be achieved by applying strain to the system. In such way, materials in which the sign of the ANC as well as the direction of the induced current change, utilizing strain, can be an interesting area for new spintronics applications. The symmetry operations of the magnetic space group of a compound determine the shape of the AHC and ANC tensors. More specifically, the Berry curvature transforms as a pseudovector under any symmetry operation, according to the formula 27 in Ref. [3].
Discussion
Since the AHC and the ANC depend on the summation of the Berry curvature in the whole Brilouin zone, they are forced to vanish for any symmetry operation that makes Berry curvature an odd function in k-space. The compounds PtNi3, CrPt3, MnPt3 belong to the same magnetic space group P4/mm'm' (BNS:123.345), which is invariant under the 2001 rotation axis (in crystallographic coordinates). This rotation axis makes the Berry curvature an odd function in k space for the ka and kc directions and therefore implies sa =sc =0. By further transforming to the standard basis of the magnetic space group (in Cartesian coordinates), we conclude that sy =sz =0, which is in complete agreement with the calculated values of the tensor (sx,sy,sz) = (s,0,0). The same method is used to extract the shape of the AHC and ANC tensors for different magnetic space groups.
