Massive Parallelization of Dynamical Multibody Systems via Co-Simulation
Jan,Kraft,Massive Parallelization of Dynamical Multibody Systems via Co-SimulationFigure 1: Partitioning of a mechanical system into coupled subsystems.
Jan KraftIntroduction
Co-simulation methods may be used advantageously for analysing complex problems, for example the simulation of systems including different physical disciplines or for the coupling of different specialized DAE/ODE solvers. In this research project, co-simulation is utilized for the purpose of parallelizing the computation of large multibody systems. Taking into account that the scaling of the computation time of multibody systems with the number of degrees of freedom is typically superlinear (depending, among other things, on the implemented formulation of the equations of motion) it brings a great benefit to split a model into coupled subsystems and compute them in parallel.
Methods
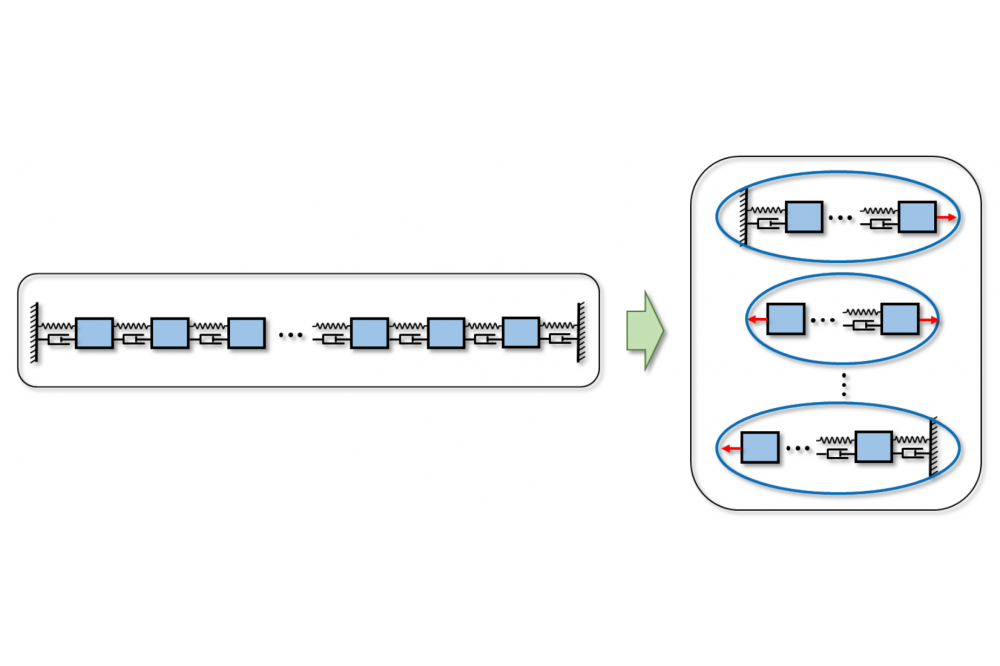
This project deals with the parallelization of multibody systems, which is achieved by partitioning the overall model into a set of coupled subsystems. The formulation of the coupling conditions between two (or more) subsystems is problem-dependent. For mechanical models, the coupling conditions can be described by constraint equations (constraint coupling) or by constitutive equations (applied-force coupling). In this work, a Jacobi-type co-simulation scheme (parallel integration of the subsystems) is used and an applied-force coupling approach to connect the subsystems is considered. The coupled problem is solved by explicit and also by implicit co-simulation techniques. Explicit methods are simpler to implement and also produce less overhead. Implicit methods usually need more subsystem information (e.g. interface Jacobians), but will be more efficient and more stable for stiff problems. The parallelized computation is obtained by a combined MPI/openMP implementation. Each subsystem is executed by an MPI-rank; if multiple integrations of the same subsystem are required (e.g. to approximate gradients or interface Jacobians), these are parallelized via openMP. All parallel threads are synchronized at specified macro-time points. Between the macro-time points, the subsystems are solved independently of each other, since a weak coupling approach is considered here. The overall computation time for a parallelized co-simulation model depends on various factors, e.g. macro-step size, number of subsystems, discontinuities in the coupling variables and overhead caused by the data transfer between the subsystems. This work focuses on the reduction of the number of macro-steps in order to increase the efficiency of a co-simulation model. Therefore, an algorithm to control the macro-step size and the order (polynomial degree) of the approximation polynomials for the coupling variables is implemented. The macro-step size controller is based on different error estimators; the order control strategy is based on the scaled derivative norm of the approximation polynomials, which is a well-established approach within classical time integration methods. The combination of macro-step size and order control allows a stable and efficient co-simulation, especially for models with strongly varying properties.
Results
Various explicit and implicit co-simulation schemes have been implemented and tested on their suitability for parallelizing dynamical multibody systems. The computation time of the test models has been strongly reduced by using a parallel co-simulation approach compared to a monolithic simulation. In addition, a macro-step size controller has been developed and implemented. The application of a non-equidistant communication time grid for sharing information between the subsystems increased the efficiency of the implemented co-simulation methods significantly. Further computation time reductions have been achieved by the implementation of an order control algorithm.
Discussion
The analysis and the reduction of the computation time using a parallel implementation of a Jacobi-type co-simulation is a challenging task because it is influenced by many factors. Besides the computational aspects like data transfer and thread synchronization in parallel computing, also the effect of the particular co-simulation method on the subsystem solvers plays an important role. For co-simulation methods the relation of the computation time and the macro-step size is not necessarily as straightforward as for classical time integration methods. Assuming that the co-simulation is carried out in parallel, the overall computation time is the sum of the subsystem integration time (i.e. of the slowest subsystem integration process) and the time required for synchronization and data exchange between the subsystems. The macro-step size can affect both parts of the overall computation time, therefore the determination of an adequate macro-step size is a key point for an efficient simulation.
