Free-Stream Coherent Structures in the Asymptotic Suction Boundary Layer
Linkmann, Moritz Free-stream coherent structures in the asymptotic suction boundary layerFigure 1: Visualisations of the streamwise averaged flow field . The colour coding represents the streamwise velocity component and the cross-flow is indicated by the superimposed arrows.
Moritz LinkmannIntroduction
The asymptotic suction boundary layer (ASBL) is a flow that develops over a flat bottom plate in the presence of suction though that plate. In consequence, the boundary layer thickness remains constant in the streamwise direction, and ASBL shares certain properties with parallel shear flows and spatially developing boundary layers. In particular, it allows the application of techniques developed for wall- bounded parallel shear flows in order to understand the dynamics of unbounded flows. Concerning the dynamics of parallel shear flows, much progress has been made in recent years through the identification of exact coherent structures, which can be travelling waves, periodic orbits or more complicated objects. Exact coherent structures in the form of travelling waves and periodic orbits have already been identified in the ASBL, where a particularly interesting feature of certain travelling wave solutions is that they extend into the free stream. As such they may be related to large-scale persistent flow structures that influence mixing and extreme fluctuations in turbulent flows, so-called turbulent superstructures. In this project, we investigate a promising type of travelling wave in order to eventually find large-scale structures that are detached from the bottom plate. To emulate an open flow in numerical simulations, a numerically necessary top plate is introduced, which must be sufficiently far away from the bottom plate to ensure that boundary effects induced by it on the region of interest remain negligible. The resulting large simulation domains and high number of computational grid points require parallel calculations.
Methods
The numerical approach used to find new coherent structures from existing ones goes under the name arc-length continuation. It consists of two main conceptual steps:
1. extrapolation: A state at a new value of the continuation parameter is obtained by polynomial extrapolation from three previously obtained structures at different values of the continuation parameter. This new state will not be a solution of the Navier-Stokes equations.
2. correction: The state obtained in the extrapolation step is used as an initial condition for a Newton search, in order to obtain a coherent structure at the new value of the continuation parameter.
Here, we continue a travelling wave in Reynolds number and with respect to the simulation domain length.
Results
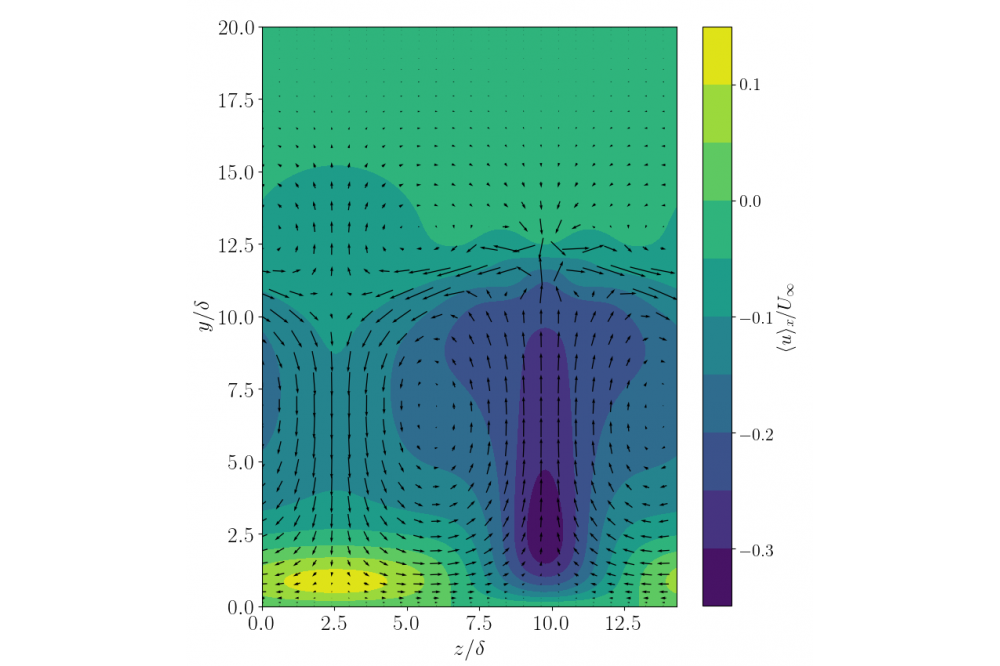
A travelling wave solution in the ASBL was continued in Reynolds number on the upper branch of its bifurcation diagram. The structure appears in a saddle-node bifurcation at Re ≈ 950. Figure 1 shows visualisations of the structure at Re = 1000 and Re = 1192, where two main features can be distinguished. (i) The slow, upwelling core of the structure, which is indicated in blue, extends up to 10δ into the free stream with almost no difference between the structures at Re = 1000 and Re = 1192. (ii) A faster upwelling region that occurs at Lx > 10δ, which grows in height with Reynolds number. This latter feature results in the box becoming eventually too low, and boundary layer effects induced by the upper wall begin to influence the dynamics markedly for Re > 1200. The structure has about 30 unstable directions at Reynolds numbers close to the location of the saddle-node bifurcation. This number increases rapidly along the upper branch, reaching 55 unstable directions at Re = 1192, which indicates the presence of a significant number of structures bifurcating off the upper branch. In order to connect the travelling wave solution to large-scale persistent flow structures that occur in wall-bounded shear flows and in boundary layers, the structure was continued in box length at a Reynolds number close to the bifurcation point from Lx = 4πδ to Lx ≈ 7.3πδ. Here, the number of unstable directions varied between 21 – 27, with the minimum attained at Lx ≈ 5.9πδ.
Discussion
The continuation in Reynolds number showed that the structure’s slow core changes little with Reynolds number. However, fast upwelling features of it extend very quickly further towards the top wall. That is, if the upper branch were to be continues further, the simulation domain must be made much higher, which requires a continuation in box height prior to a continuation in Reynolds number. The large variation in the number of unstable directions along the upper branch motivates further searches for structures bifurcating off the upper branch. However, as candidates for a description of turbulent superstructures, the ECS would need to be calculated in longer simulation domains. That is, altogether the present results call for further studies concerning the presence of travelling waves and other ECS such as periodic orbits in long simulation boxes and their relevance to turbulent superstructures in the ASBL.
