Ab Initio Calculations on the Intrinsic Spin Hall Effect

Fabian, Alexander, ab initio calculations on the intrinsic Spin Hall eﬀect, Figure 1

Figure 1: Averaged spin polarization of a platinum thin ﬁlm in the middle region. On the left and right hand side the continuation in the leads is indicated.

Alexander Fabian

Fabian, Alexander, ab initio calculations on the intrinsic Spin Hall eﬀect, Figure 2

Figure 2: Variation of the magnetization with distance in z direction.

Alexander Fabian

Introduction

The ﬁeld of spintronics recently gained much interest because it promises faster, smaller and less energy consuming devices replacing or aiding the current electronic ones. In electronics normally, only the charge of the electron is used for transferring and processing information. However, electrons have another degree of freedom that can be used which is the electronic spin. In order for such devices to work properly, one needs spin-polarized currents, that is a current in which only one of the two sorts of spins is present. The Spin Hall eﬀect can provide such spin-polarized currents when an electrical voltage is applied to certain materials. On the opposing surfaces of this material, the two spin sorts accumulate and can be injected into the device.

Methods

We use a Korringa Kohn Rostoker (KKR) density functional theory (DFT) method to calculate the spin accumulation self consistently. The system, here a platinum slab, is divided into three parts. Left and right leads are in equilibrium and serve as an electron reservoir. The middle region is the actual device, where the eﬀect will happen. Since a charge current is needed to obtain the spin current, we apply a bias voltage on both sides. The self-consistent potential is then solved by the standard DFT iteration process. The necessary energy integrals are calculated by dividing the path into an equilibrium part and a non-equilibrium part. Doing so we can reduce the computational cost of the overall calculation. By ﬁnally obtaining the electronic density for spin-up and spin-down we ﬁnally ﬁnd the magnetization for each atom of the system.

Results

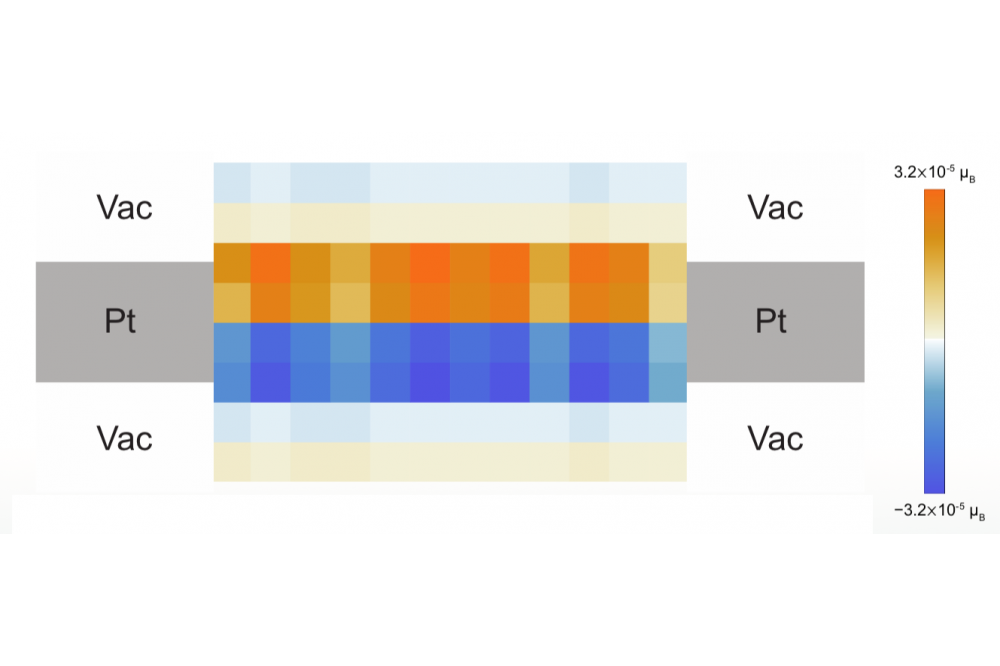
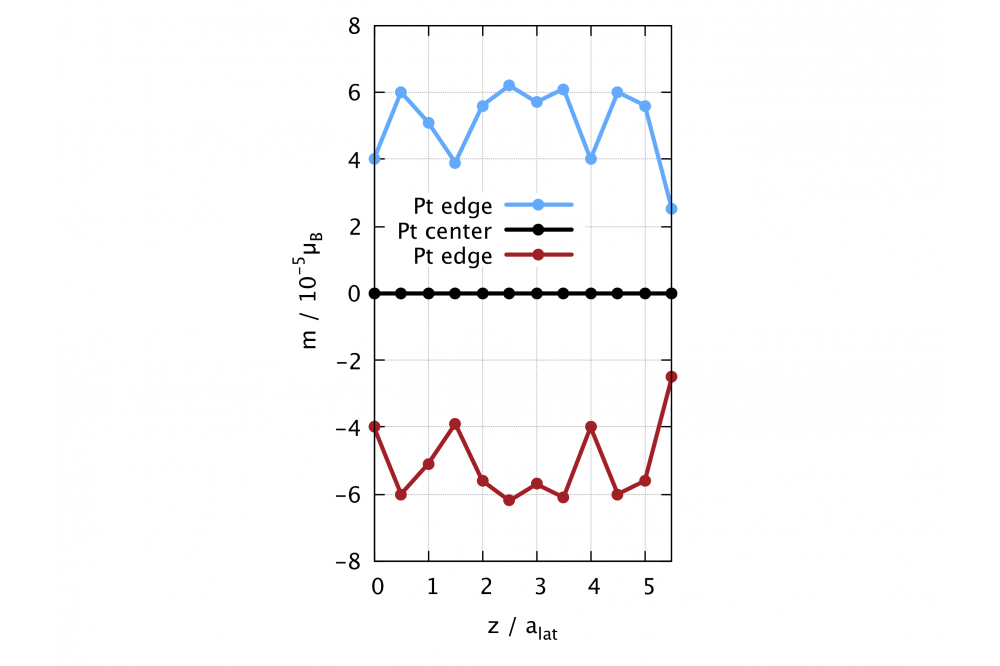
The system under consideration is a platinum surface slab modeled as in-plane supercell (perpendicular to the transport direction (out-of-plane direction)). The results for the magnetization are plotted in ﬁgure 1 and 2. It can be clearly seen, that the results are symmetric regarding the opposing platinum atoms. The center platinum atom cell shows no magnetization. Maximum values vary between ±6x10^-5 μ_B. However, oscillations of the magnetization in the transport direction occur.

Discussion

The symmetry of magnetization values for opposing platinum atoms is to be expected. The positive and negative values together with the absolute value being the same ensure, that the total magnetization is zero. This means no magnetization has been created, but only spin up and spin down electrons have been separated. Due to our method, we get small discontinuations of the potentials in the transport direction. This could give rise to the occurrence of quantum size eﬀects. Hence it would explain the oscillations in the transport direction.

Outlook

The presented calculations have shown that in principle using a full relativistic DFT ansatz it is possible to directly calculate the spin accumulation caused by the Intrinsic spin Hall eﬀect. Further work should consider larger cells for a more realistic description. The occurrence of oscillations in the magnetization have to be further analyzed to conﬁrm they are quantum size eﬀects. For future work, a means of determining the spin Hall angle has to be found. Moreover, realistic scattering could be considered by using scattering time formalism with virtual terminals.

HKHLR - HPC Hessen