Data Synthesis for Large-Scale Hydrodynamic Model Inference
Lukas_Hecht_Data Synthesis for Large-Scale Hydrodynamic Model Inference_Figure1Figure 1: Schematic overview of the project. A machine learning model is trained using numerical solutions (simulation videos) of about 600 different PDEs. The objective is to train an artificial neural network to predict a partial differential equation from a given input movie. The equation on the right represents an exemplary prediction with coefficients α, β, κ, λ, χ.
Lukas_Hecht_Data Synthesis for Large-Scale Hydrodynamic Model Inference_Figure2Figure 2: Exemplary solutions of the active model B+ (a–c), the Cahn-Hilliard model (d–f), and the Swift-Hohenberg equation (g–i) obtained from simulations performed on the Lichtenberg II high performance computer. From left to right we show the initial condition, the 40th frame, and the 80th frame.
Lukas_Hecht_Data Synthesis for Large-Scale Hydrodynamic Model Inference_Figure3Figure 3: Effect of training dataset size on the accuracy of the machine learning model. We trained individual instances of our machine learning model on datasets of progressively increasing size. Each of the resulting models was subsequently evaluated on a distinct test set comprising approximately 16×103 data points (videos). In this context, the model accuracy is defined as the average percentage of correctly predicted differential terms per video. Both the training and test datasets were synthetically created by varying the initial conditions of the “generating equation” via the data engine.
Introduction
Continuum models are of utmost importance in different fields of research and are often used to describe the macroscopic behavior of physical systems. A key area of interest is the study of collective behavior observed in active matter systems using continuum models. These systems, that consume energy from their surrounding to propel themselves, in many cases give rise to interesting collective phenomena such as pattern formation or motility induces phase separation. In most cases, employing particle-based approaches to describe these systems imposes inherent limitations on both the temporal and spatial scales under investigation. By contrast, continuum models present the potential to overcome these constraints. However, a systematic and well-defined computational methodology to formulate partial differential equations (PDEs) that characterize continuum models for active matter systems is still elusive. Although several phenomenological methods have been developed historically—for instance by leveraging the system’s symmetries and conservation laws—there is no assurance that these models comprehensively incorporate all the necessary terms to accurately describe the system’s dynamics. Recently newer families of data-driven and machine learning based methods have been suggested for approaching this problem. However, most of these methods still rely on hand-crafted features of the system (such as the computed derivatives), which in return introduces another layer of complexity to the final approach. In this project, we aimed at designing an end-to-end machine learning model that is capable of inferring the coefficients of the PDE terms for a given system from data (videos). As can be imagined, a solution at this level would require a large amount of data, for which we developed a a PDE solver which we refer to as data engine, which enabled us to synthesize numerical solutions for a given family of PDEs. Using the resources granted by the Lichtenberg II, we generated a large dataset of different PDEs and used this synthesized data to train our model.
Methods
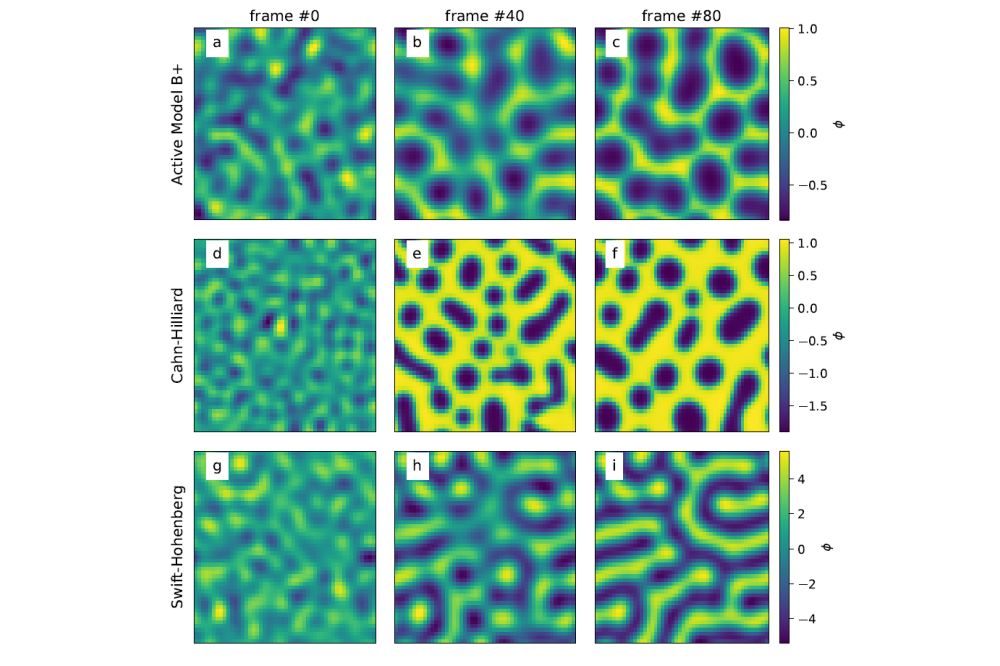
To achieve our goal, we first designed and developed the data engine program which could synthesize solutions for any PDE in the form ∂tϕ = aϕ + bϕ3 + c∇ϕ + d∇2ϕ + e∇2ϕ2 +f ∇2ϕ3 +g∇4ϕ+h∇2(∇ϕ)2 +j∇·[(∇2ϕ)∇ϕ] (called “generating equation” hereafter), where a, b, c, d, e, f, g, h, j are free parameters and ϕ(x, t ) is a field that depends on space x and time t. Here for a given parameter set and an initial field ϕ0(x, t ) = ϕ(x, 0), the data engine generates a solution (movie, typically with 81 frames) which, coupled with its underlying PDE, produces one instance of the training or test data for our machine learning model. One could easily imagine several sub-families of important PDEs which can be directly generated from the above “generating equation”, such as the Swift-Hohenberg, Cahn-Hillard, and Active model B+. For each dataset, we partitioned the data into training and test sets, ensuring that initial conditions (PDE parameters and ϕ0) were entirely distinct between the two groups.
Results
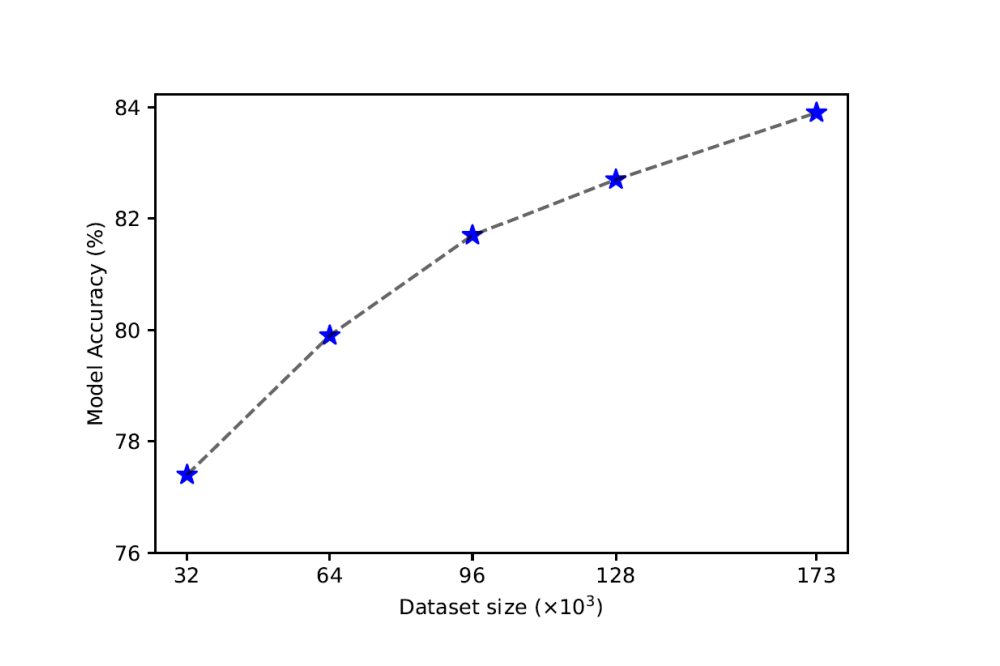
Using the resources granted to us during the project, we produced several auxiliary datasets which helped us better design the machine learning model. Subsequently, we extended the scope of our analysis to evaluate the performance of the model in a broad spectrum of PDE families. For this, we considered various combinations of parameters within the above “generating equation”, which in total give rise to 639 different PDEs in the final datasets. We then generated a large dataset comprising approximately 173k training and 16k test datapoints (videos) with various parameter and initial condition regimes for these PDEs and tested the model’s performance. Interestingly, despite the formidable complexity of handling more than 600 different partial differential equations, the machine learning model maintains a high level of accuracy. It effectively identifies the specific PDE type by inferring its constituent terms while simultaneously estimating the associated coefficient values with significant precision. We also observed continuous improvement in accuracy as we scaled the size of the training dataset. This general trend hints at the crucial role of the size and diversity of the synthesized training dataset in the final performance of the model.
Discussion
Currently, there is no robust and generic learning approach for systematically obtaining governing equations for active matter systems from data. During this project we developed the necessary steps to synthesize a large-scale dataset for training our end-to-end machine learning model. We generated a dataset comprising of approximately 190k datapoints (videos) for more than 600 different PDEs with various initial conditions. Our machine learning model demonstrated robust performance and straight-forward scalability with respect to the training dataset size. As a next step, we plan to study the role of inner class (PDE type) generalizability of our machine learning approach and aim to apply our model to learn PDEs from experimental data and particle based simulations.
