Hypergraphon Mean Field Games
Kai_Cui_Hypergraphon Mean Field Games_Figure1Figure 1: An example hypergraph is transformed into a multi-layer uniform hypergraph and their associated (step-)hypergraphons.
Kai CuiIntroduction
Recent developments in the field of complex systems have shown that real-world multiagent systems are often not restricted to pairwise interactions, bringing to light the need for tractable models allowing higher-order interactions. At the same time, the complexity of analysis of large-scale multi-agent systems on graphs remains an issue even without considering higher-order interactions. An increasingly popular and tractable approach of analysis is the theory of mean field games. We combine mean field games with higher-order structure by means of hypergraphons, a limiting description of very large hypergraphs. To motivate our model, we build a theoretical foundation for the limiting system, showing that the limiting system has a solution and that it approximates finite, sufficiently large systems well. This allows us to analyze otherwise intractable, large hypergraph games with theoretical guarantees, which we verify using two examples of rumor spreading and epidemics control Our contribution can be summarized as follows: (i) To the best of our knowledge, ours is the first general mean field game-theoretical framework for non-linear dynamics on multi-layer hypergraphs. Multi-layer networks have proven extremely useful in many application areas including infectious disease epidemiology, where different layers could be used to describe community, household and hospital settings. (ii) We prove the existence and the approximation properties of the proposed mean field equilibria. (iii) We propose and empirically verify algorithms for solving such hypergraphon mean field systems, and thereby obtain a tractable approach to solving and analyzing otherwise intractable Nash equilibria on multi-layer hypergraph games. The proposed framework is of great generality, extending the recently established graphon mean field games and thereby also standard mean field games (via fully-connected graphs).
Methods
The goal of our work is the synthesis of dynamical systems on hypergraphs with competitive or selfish agents. Existing analysis of hypergraph mean field systems typically remains restricted to special dynamics such as epidemiological equations or opinion dynamics on sparse graphs. In contrast, our work deals with general, agent-controlled non-linear dynamics and equilibrium solutions. We build upon prior results for discretetime, graph-based mean field systems and extend them to incorporate higher-order hypergraphs as well as multiple layers.
Results
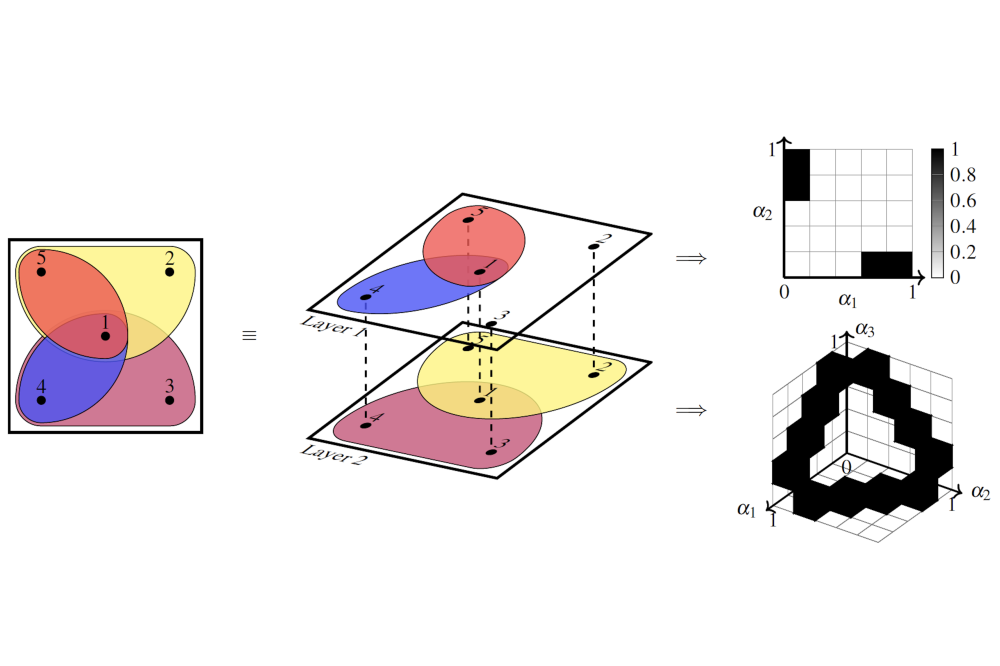
We find that it suffices to define and consider hypergraphs as multi-layer hypergraphs, where each layer is given by a uniform hypergraph, see also Fig. 1 for a visualization. For instance, in social networks each layer could model e.g. the k-cliques of acquaintances formed at work, friendship at school or family relations. To formulate the infinitely-large mean field system, we define the limiting description of sufficiently dense multilayer hypergraphs as the graphs intuitively become infinite in size, called hypergraphons. We formulate a dynamical model on hypergraphs where each node is understood as an agent that is influenced by the state distribution of all of its neighbors, according to some time-varying dynamics. Furthermore, each agent is expected to selfishly optimize its own objective, which gives rise to Nash equilibria. Our goal is now to find Nash equilibria, i.e. stable policies where no agent can singlehandedly deviate and improve their own objective. We rigorously motivate the mean field formulation by providing existence and approximation results. In order to learn an equilibrium in our model, we shall adopt a discretization method to convert the graphon mean field game into a classical mean field game, and thereby allow application of any existing mean field game algorithms such as fixed point iteration to solve for equilibria. In our experiments, we restrict ourselves to finite time horizons and use backwards induction with exact forward propagation to compute exact solutions. Note that simple fixed point iteration by repeatedly computing an arbitrary optimal deterministic policy and its corresponding mean field converges to an equilibrium in one problem we consider. In general however, fixed point iteration (as well as more advanced state-of-the-art techniques) may fail to converge, as seen by another problem we consider. We verify theoretical results and find qualitatively correct equilibrium behavior in our experiments. Overall, we find that multi-layer hypergraphon mean field games allow for more complex behavior and modelling of connections than a single-layer graphon approach.
Discussion
In this work, we introduced a model for dynamical systems on hypergraphs that can describe agents with weak interaction via the graph structure. The model allows for a rigorous and simple mean field description that has a complexity independent of the number of agents. We verify our approach both theoretically and empirically on a rumor spreading example. By introducing game-theoretical ideas, we thus obtain a framework for solving otherwise intractable large-scale games on hypergraphs in a tractable manner.
