Improving the Model-Based Prediction of Vibroacoustic Vehicle Properties by Mastering Uncertainty
Xu_Wei_Improving the Model-Based Prediction of Vibroacoustic Vehicle Properties by Mastering Uncertainty_Figure1Figure1: Result of sensitivity analysis. The horizontal axis shows the model parameters, while the vertical axis denotes the total Sobol Indices of parameters regarding 4 quantities of interests. Young’s Modulus Esheet, density ρsheet, and thickness tsheet are sensitive to 4 Eigenfrequencies due to higher total Sobol Indices.
Wei Xu
Xu_Wei_Improving the Model-Based Prediction of Vibroacoustic Vehicle Properties by Mastering Uncertainty_Figure2Figure 2: Result of scalability test. Abscissa and ordinate denote the Nastran High performance settings, distributed memory parallel (DMP) and shared memory parallel (SMP), while applicate is the performance of the strategy via combinations of DMP - and SMP settings.
DMP 4 + SMP 4 is the best strategy due to minimal elapsed time and medium CPU, memory usage, which means multiple simulations can be parallel started on 1 computation node.
Introduction
Vibroacoustic vehicle behavior specifies among others the quality of vehicles and contributes to customer satisfaction. In the early design phase, model-based analysis using a finite element (FE) model is conducted to predict the properties and to design the vibroacoustic vehicle behavior. Deterministic models are unable to include the variances due to manufacturing tolerances and lead to an incomplete determination of the real vibroacoustic behavior of a vehicle. Probabilistic models raise many research of interests, however, the time-consuming large-scale simulations limit their applicability. The Lichtenberg High-Performance Computing (HPC) provides sufficient computational resources. Monte-Carlo simulations for industrial FE models can therefore be performed, where a large number of parameter samples are drawn from probability space and are assigned to an industrial FE model to get the probabilistic model-based predictions. In addition, parallel computing strategies can be utilized to accelerate the computations.
Methods
A Matlab interface for Monte-Carlo simulations including modifying parameters, executing Nastran, interacting with HPC as well as postprocessing is developed and tested by simulating a simplified industrial FE model of a vehicle luggage compartment floor. The probability space for model parameters like density and Young’s Modulus is constructed by uniform distributions, Monte-Carlo simulations are performed based on samples to get the vibroacoustic model-based predictions. The large-scale simulations are accelerated by parallel computation using Matlab Parallel Computing Toolbox. Variance based global sensitivity analysis is performed to investigate the influence of parameters on model-based predictions. Dominant model parameters that have greater effect are determined, which drive the FE model update using Bayesian-based parameter calibration.
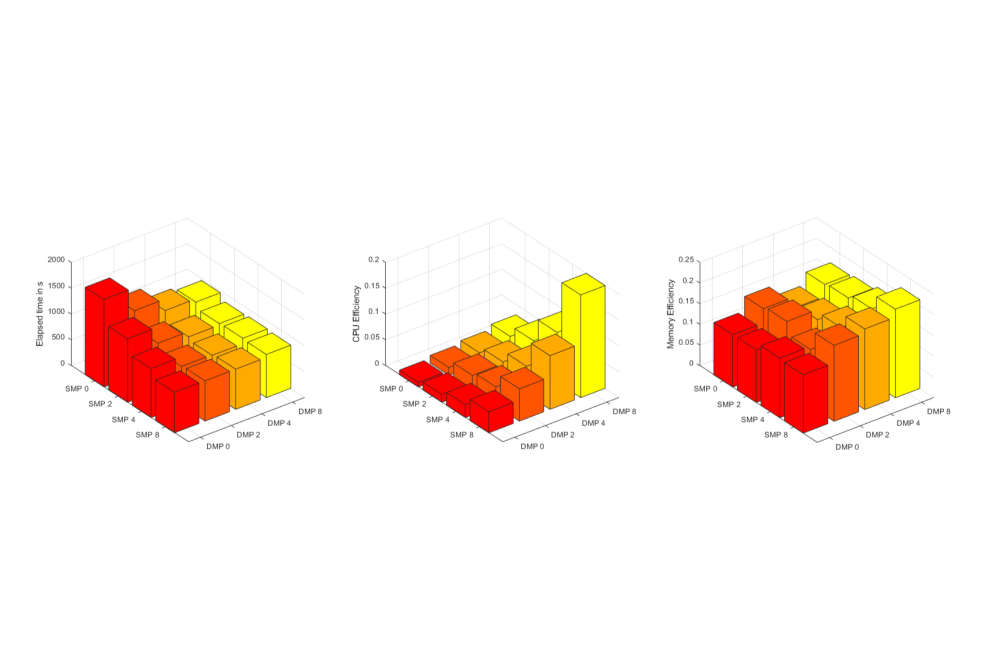
As the complexity of a vehicle luggage compartment floor is relatively small, a single simulation can be finished in seconds. When a full industrial model like an entire car body is treated, the computational cost increases drastically. In order to make full use of the computational resources, a scalability test is executed to find a set of optimal configurations in terms of Nastran High Performance Computing setting for Monte-Carlo simulations of the entire vehicle body. Here, a two-dimensional optimization problem is considered: Minimize the computational time by finding a Distributed Memory Parallel (DMP) - Shared Memory Parallel (SMP) configuration in Nastran, followed by observing the CPU-efficiency and the memory-efficiency.
Results
In terms of the simplified industrial FE model, 10,000 samples of uniformly distributed input parameters are assigned for parallel Monte-Carlo simulations. The computation finished in 2 hours using 2 computation nodes. After the simulations, sensitivity analysis is conducted. The result is presented in the following section with corresponding figures.
In terms of the full industrial FE model, a set of optimal configuration parameters is found, namely “DMP4 + SMP4”. The computation of single simulation with these setting is finished in 12 min 30s (750s). The result is presented in the following section with corresponding figures.
Discussion
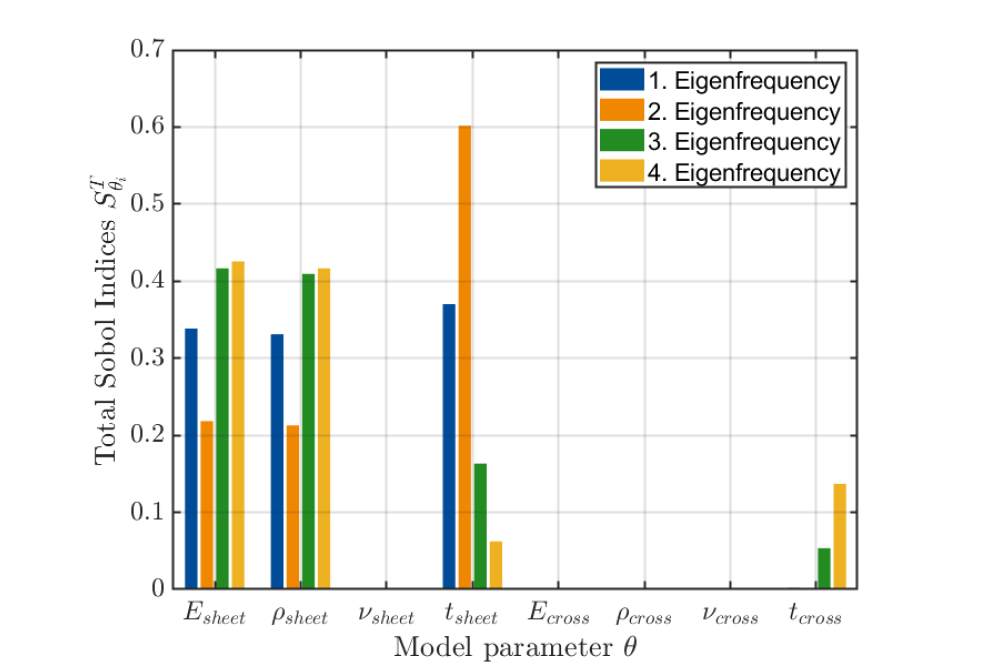
In terms of the simplified industrial FE model, by using HPC and parallel computation for Monte-Carlo simulations, the computation time for 10,000 simulations is reduced by 86% compared to the sequential simulations (2 h vs. 13.9 h). Via Sensitivity analysis, three dominant parameters Young’s Modulus Esheet, density ρsheet, and thickness tsheet of floor sheet are selected from parameter space, which are influential for the 1. – 4. natural frequencies. These parameters are sensitive for predicting vibroacoustic vehicle properties and will be calibrated for model update.
The optimum configuration parameters are different for different models, and it is necessary to conduct a scalability test to find the optimum configuration parameters before performing large-scale simulations, especially for the complex model. In terms of the full industrial FE model, the computational time reduces by 52% after determining Nastran High Performance Setting DMP4 + SMP4 via scalability test. These setting will be further used for Monte-Carlo simulations of the entire vehicle body, to complete the sensitivity analysis and model update within an acceptable computational time.
Extra judgment criteria have been added to the Matlab script to handle exceptions such as “out of memory” errors to increase the robustness of the workflow. Currently, the entire workflow is capable for a robust large-scale Monte-Carlo simulations of industrial FE models.
In the follow-up project, Bayesian based parameter calibration for model update will be conducted based on the Monte-Carlo simulations, in order to improve the quality of model-based predictions by quantifying data uncertainty. The progress and results will be the basis for the following NHR-NORMAL project, to perform the large-scale Monte-Carlo simulations and uncertainty quantification for full industrial FE model like entire vehicle body.
