Gitter-QCD-Untersuchung von Tetraquark-Kandidaten
Einleitung
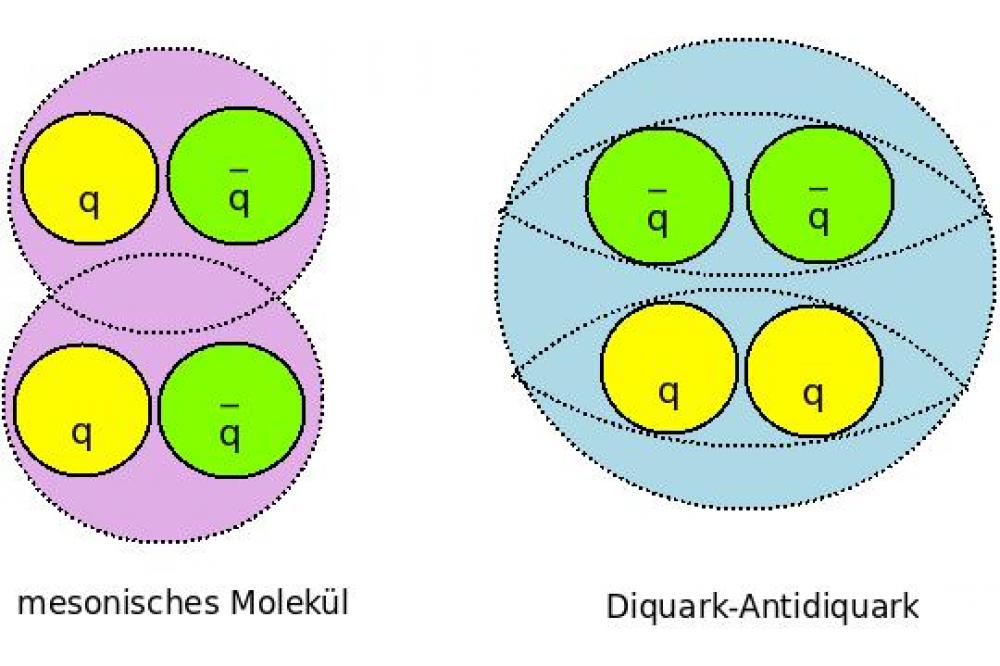
Die Quantenchromodynamik (QCD), die Theorie der Quarks und Gluonen, beschreibt den Aufbau eines Großteils der uns umgebenden Materie. Zum Beispiel bestehen sowohl Proton als auch Neutron aus drei Quarks, die von Gluonen zusammengehalten werden. Gebundene Zustände von Quarks werden allgemein als Hadronen bezeichnet. Man unterscheidet zwischen Mesonen (typischerweise gebundene Quark-AntiquarkPaare) und Baryonen (gebundene Zustände aus drei Quarks). Tetraquarks sind viel diskutierte, möglicherweise existierende mesonische Zustände, die aus zwei Quarks und zwei Antiquarks bestehen. Tetraquarks bieten eine Erklärung für eine Reihe unbeantworteter Fragen im Bereich der Mesonphysik. Neben der Existenz und den Massen von Tetraquarks ist auch deren Struktur von Interesse, da unterschiedliche Möglichkeiten diskutiert werden, wie die Quarks in einem Tetraquark angeordnet sind. Ist die Bindung zwischen jeweils einem Quark und einem Antiquark stark, spricht man von einem mesonischen Molekül. Bei einer starken Bindung zwischen den beiden Quarks und den beiden Antiquarks liegt ein Diquark-Antidiquark vor (Abbildung 1).
Methoden
Das Hauptziel dieses Projekts besteht darin, ein besseres qualitatives Verständnis von möglicherweise existierenden Tetraquarks zu gewinnen. Unsere Arbeitsgruppe verfolgt dabei zwei komplementäre Ansätze.
- Zum einen werden konzeptionelle Untersuchungen in technisch vergleichsweise einfachen Systemen durchgeführt, bei denen zwei der vier Quarks als unendlich schwer angenommen werden. Mit Hilfe von numerischen Gitter-QCD-Rechnungen kann bestimmt werden, welche anziehenden beziehungsweise abstoßenden Kräfte zwischen zwei Mesonen auftreten.
- In einem zweiten Schritt wird dann mit quantenmechanischen Modellrechnungen überprüft, ob diese Kräfte stark genug sind, um vier Quarks zu einem Tetraquark zusammenzubinden.
Ergebnisse
Erste Ergebnisse hierzu sind vielversprechend: Es wurden starke Anzeichen dafür gefunden, dass zwei schwere B-Mesonen in einer speziellen Anordung einen gebundenen Vier-Quark-Zustand bilden können, also ein Tetraquark[1-4]. Gegenwärtig werden diese Rechnungen für den experimentell interessanteren aber gleichzeitig technisch schwierigeren Fall eines B- und eines Anti-B-Mesons erweitert. Außerdem is eine Verfeinerung der erwähnten quantenmechanischen Modellrechnungen in Arbeit. Unser zweiter Ansatz besteht in der Berechnung und Analyse sogennanter Korrelationsmatrizen von Tetraquark-Operatoren. Dabei werden bei vorgegebenen Quantenzahlen die möglichen Strukturen eines Tetraquarkkandidaten (z.B. mesonsiches Molekül und Diquark-Antidiquark (Abb. 1), aber auch Quark-Antiquarkund nichtgebundene Zwei-Meson-Zustände) durch eine Reihe von Operatoren modelliert. Diagrammatisch ist eine typische Korrelationsmatrix in Abbildung 2 skizziert. Aus ihr können Informationen über die Masse und Struktur des a_0(980)-Mesons extrahiert werden. Die numerische Berechnung der Korrelationsmatrix ist jedoch ausgesprochen aufwändig, da sie in etwa der Lösung eines einhundertmillionen-dimensionalen Integrals entspricht. Gegenwärtig sind Teile der in Abbildung 2 gezeigten Matrix verfügbar.[5-11] Eine entsprechende Analyse hat gezeigt, dass es sich beim a_0(980)-Meson nicht um einen stabilen Vier-QuarkZustand handelt.[6]
Diskussion
Um weitere Informationen über die Struktur des a_0(980)-Mesons zu erhalten, werden momentan die verbleibenden Diagramme aus Abbildung 2 berechnet. Geplant ist außerdem die Verwendung des entwickelten Codes zum Studium schwererer Tetraquark-Kandidaten aus dem D- und D_s-Meson- und dem Charmonium-Sektor, wie sie voraussichtlih auch in näherer Zukunft mit dem PANDA-Experiment am FAIRBeschleuniger experimentell untersucht werden.