Designing Materials With Photo-Induced Phase Transitions
Einleitung
The potential of chalcogenides in applications like optoelectronics, thermoelectrics, transparent contacts, and thin film transistors, is explored in this project. Chalcogenides offer higher mobility and p-type dopability compared to oxides, thanks to their covalent metal-X bonds and higher-energy valence bands from p-orbitals. The relatively low number of synthesized chalcogenides hints at undiscovered ones with unique properties. To address this, we use a systematic high-throughput screening process and first-principles calculations on ternary chalcogenides, creating a database of over 400,000 compounds. High-performance computing (HPC) accelerates computation and analysis, aligning with recent improvements in density functional theory (DFT) simulations.
Methoden
The first-principles calculations were performed using an in-house-developed HTP calculation environment. All the calculations were carried out within the DFT framework, as implemented in the Vienna ab initio simulation package. The interaction between core and valence electrons was explained using the frozen-core projector-augmented wave pseudopotentials. In our calculations, the generalized gradient approximation with Perdew–Burke–Ernzerhof (GGA-PBE) functional was used as the exchange–correlation functional. The crystal structures were fully optimized with the energy convergence criteria of 1 × 10–5 eV. The kinetic energy cutoff for plane-wave basis was set to 500 eV, in conjunction with a grid spacing of 2π × 0.03 ˚A−1 for Brillouin zone sampling. Given the significance of scaling the convergence standard with the number of atoms, we conducted convergence tests concerning the self-consistent field convergence criterion, kinetic energy cutoff, and k-point grid spacing for structural optimization.
Ergebnisse
1. High-throughput Calculation of Band Gap
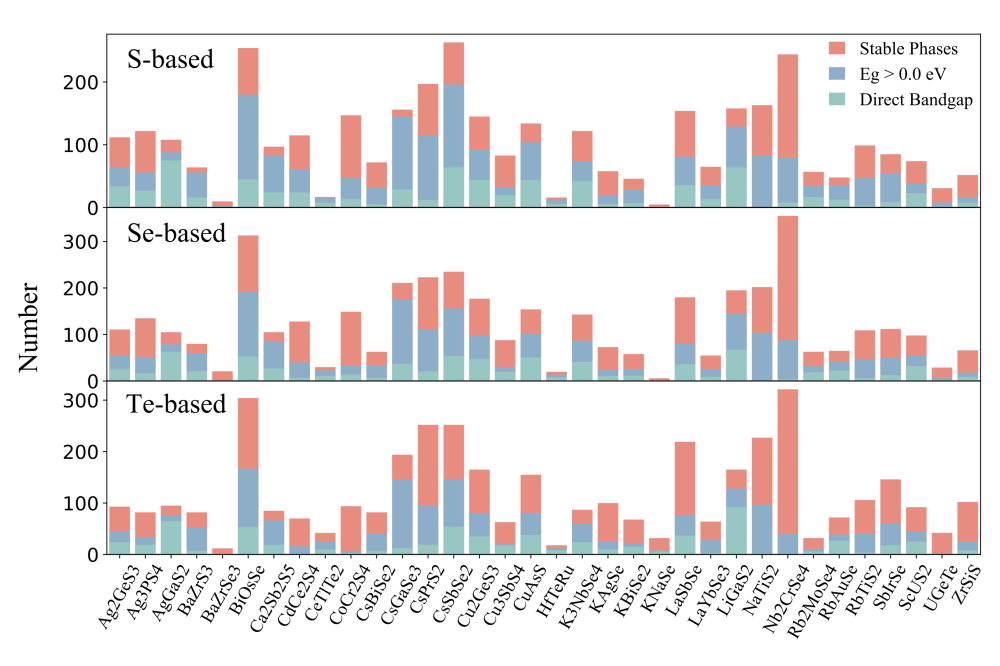
The Shockley-Queisser (S-Q) efficiency limit suggests that the ideal band gap (Eg) of a solar absorber in a single-junction cell should be approximately 1.34 eV. To accelerate the screening process for potential candidates, a low computational cost method is required. Therefore, we evaluate the thermodynamic stability of all ternary candidates and calculate the band gap of 1417 stable phases and 8023 metastable phases using the approximate GGA-PBE exchange functional. It should be noted that the GGAPBE functional tends to underestimate the band gap by 0.5-0.6 eV. Considering the subsequent investigation for diverse optoelectronic applications, a preliminary screening criterion was set at Eg > 0 eV, resulting in a reduced number of ternary candidates to 6140.
To obtain accurate electronic band gap values for the remaining candidates, high-throughput calculations are performed using the scPBE0 functional. We conducted benchmarks on experimentally-known materials, such as CdTe and ZnX (X=O, S, Se, and Te), to compare the experimental and theoretical band gap results.
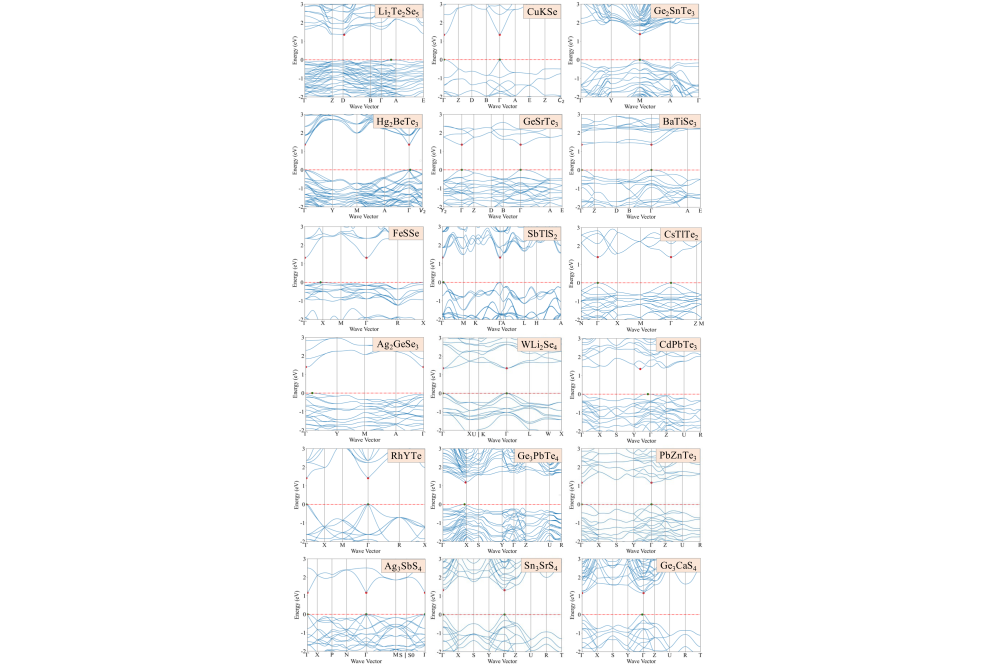
The analysis shows that structural prototypes like AgGaS2 or LiGaS2 with corner-sharing AX4 and BX4 tetrahedra tend to have direct band gaps, which is crucial for optoelectronic performance. Smaller gap differences (ΔEg) reduce nonradiative recombination loss, enhancing photovoltaic efficiency. We focused on chalcogenides with 0.8-2.0 eV band gaps and ΔEg ¡ 0.2 eV, narrowing candidates down to 1477. However, intrinsic defects and impurities can harm efficiency by causing nonradiative carrier recombination via localized trap states. Investigating defect physics is computationally intensive and will be explored in future studies.
2. Photovoltaic Performance and Electronic Structures
After obtaining the band gap and stability of chalcogenides, their potential as photovoltaic materials can be roughly evaluated based on the S-Q limit. Typically, a promising absorber for solar cells exhibits direct bandgap characteristics, enabling strong optical absorption with reduced thickness. However, the conventional evaluation of S-Q efficiency solely based on band gap value may overlook dipole-forbidden direct transitions in some direct-gap materials. Thus, to address this limitation, the ”Spectroscopic Limited Maximum Efficiency (SLME)” is adopted as a target property to assess candidate efficiency.
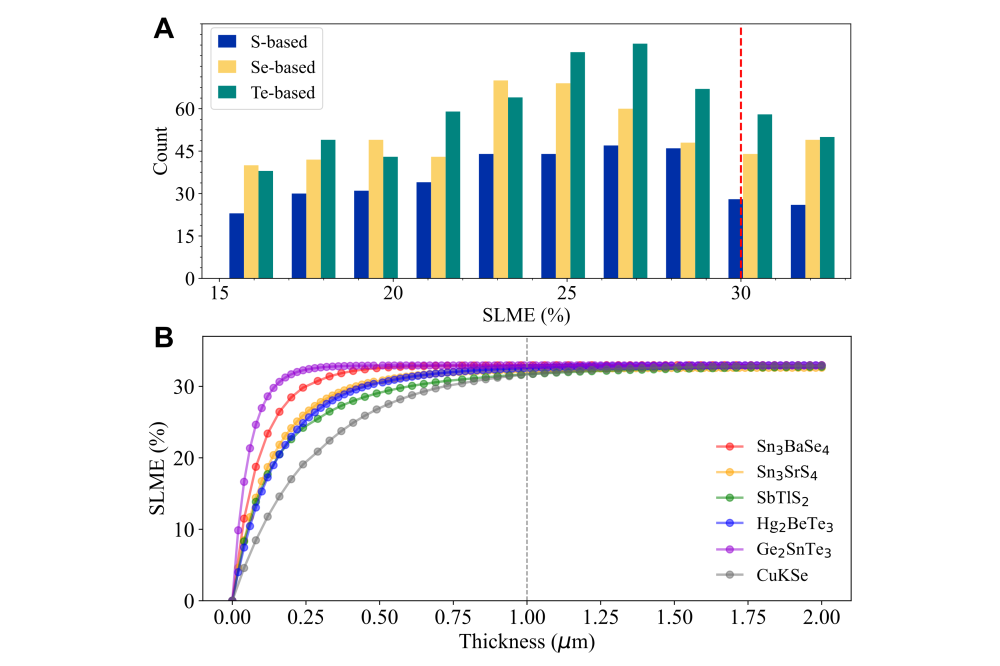
We calculated SLME for candidates with band gaps from 0.8 to 2.0 eV using a 2 µm film thickness and standard AM1.5G solar spectrum illumination. GaAs, CdTe, and CuGaSe2 SLME values matched experimental data, confirming our predictions’ reliability. Among chalcogenides, 15, 32, and 35 candidates achieved ≥32% theoretical efficiencies for S-, Se-, and Te-based materials.
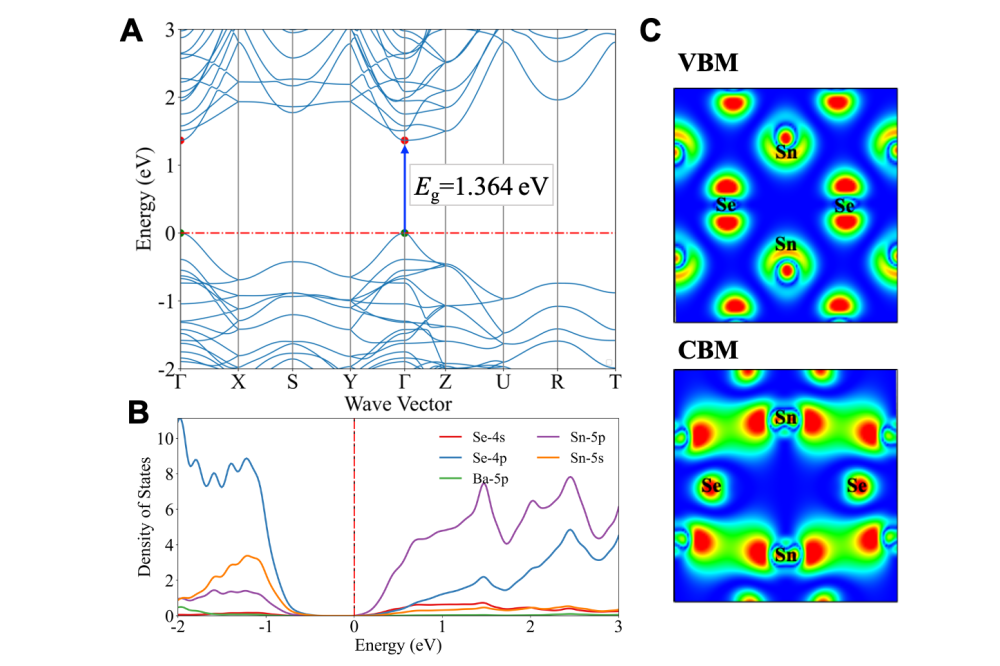
For insight into candidate mechanisms, we examined Sn3BaSe4 which has a 1.364 eV direct band gap, ideal for single-junction solar cells, with high carrier mobility (0.08 m0 for holes m∗h and 0.20 m0 for electrons m*e). The valence band is primarily Sn-s and Se-p orbitals, while the conduction band combines Sn-p, Se-p, and Se-s orbitals. Analysis of crystal orbital populations shows unique Sn-Se chemical bonding with distinctive lone-pair Sn-5s2 electronic configuration. Similar configurations exist in candidates like Ge2SnTe3 and SbTlS2, making them promising lead-free alternatives for optoelectronic applications. However, further investigations are needed to explore their detailed properties and performance.
Diskussion
In summary, we have presented a comprehensive high-throughput screening process based on the idea of ion substitution and ab initio calculations to explore promising ternary chalcogenides for optoelectronic applications. By replacing A- and B-site cations in ternary AxByXz chalcogenides crystallized in 34 structural prototypes, a rich material database containing > 400,000 AxByXz chalcogenide candidates was constructed. After a series of systematic first-principles calculations, we found 7943 unknown materials exhibiting satisfactory phase stability against chemical decomposition. On this basis, the chemical distribution of phase stability in terms of the structural prototype and chemical composition was established.