Flow Regimes within Horizontal Particle-Laden Annular Pipe Flows
Xiaoyu Wang_Flow regimes within horizontal particle-laden annular pipe flows_fIgure 1Flow regimes classification with different rotation rates N.
Einleitung
The understanding of particle-laden flows, particularly gas-solid flows in horizontal annular pipes, remains limited despite their broad engineering relevance. The restricted progress in this field is largely attributable to the lack of systematic investigations into the relative importance of the dimensionless parameters governing these flows. In addition to the flow Reynolds number, the dominant control parameters include the mass loading ratio, the density ratio and the particle Stokes number. The horizontal annular configuration is further complicated by the combined effects of gravity and inner cylinder rotation. These are quantitatively represented by the Froude number and the non-dimensional wall rotation rate varying with different values.
Methoden
The governing momentum equation for the velocity field within the unsteady sensitized RANS framework is expressed with the unknown Reynolds stress tensor. In the conventional RANS-RSM approach, this tensor is obtained from a differential near-wall second-moment closure model, representing the fully-modeled contribution of the Reynolds stress tensor, it instead corresponds to the stress tensor associated with the unresolved residual fine scale turbulent structures within the sensitized-RANS methodology. Within the framework of the latter approach, denoted as the Improved Instability-Sensitive Reynolds Stress Model (IIS-RSM), the transport equation of the specific dissipation rate, incorporates an additional production source term, formulated in terms of the second derivative of the underlying velocity field. Such a formulation allows the model to adequately capture turbulence fluctuations consistent with the resolved unsteady turbulence content, in analogy with the Scale-Adaptive Simulation (SAS) concept. The motion of particles with densities much greater than that of the carrier fluid and diameters smaller than the Kolmogorov length scale is governed by the momentum transport equation, with force models accounting for the drag force, the gravitational and buoyant forces and the Saffman lift force. In the present cases, where particle volume fractions are high and particle sedimentation and aggregation play a significant role, a four-way coupling strategy is adopted. Interactions involving both inter-particle and particle-wall collisions are effectively modeled using the spring-slider-dashpot approach.
Ergebnisse
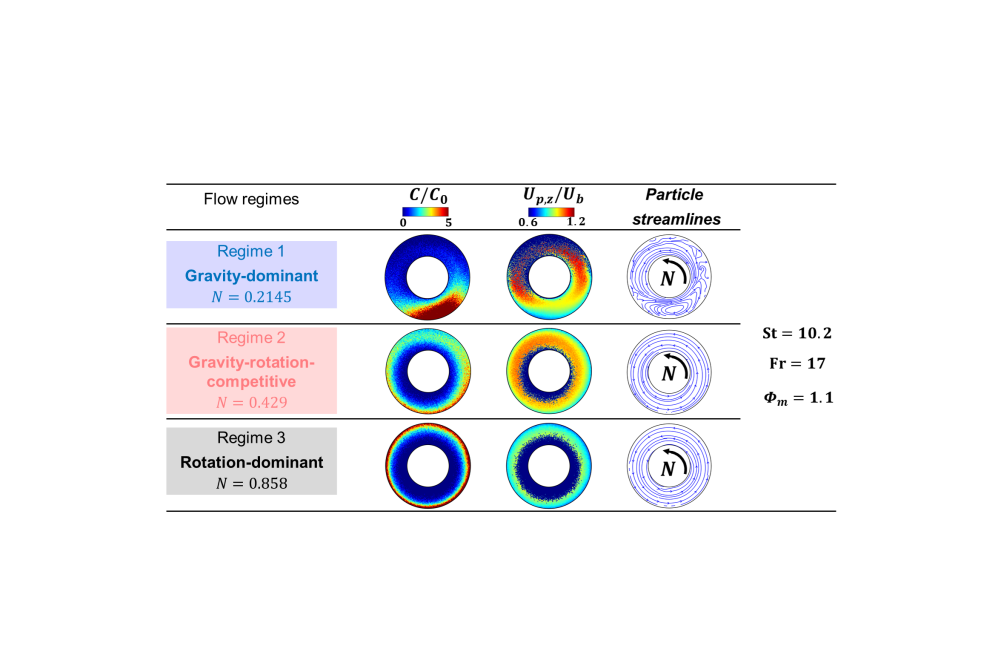
Figure 1 illustrates three distinct flow regimes that can be classified depending on the combination of N, St, Fr and Φₘ. In Regime 1 (gravity-dominant), particle concentration profiles exhibit a slight vertical asymmetry, with the majority of particles accumulating in the lower half of the annulus. This gravitational bias manifests in the streamwise particle velocity, which is higher in the upper left region and reduced in the lower right region. The particle streamlines in the (r-θ) plane reveal that a significant fraction of particles fail to reach the upper half of the annulus, leading to a vortex structure in the lower region, directly attributable to sedimentation effects. In Regime 2 (gravity-rotation-competitive), particles are distributed across the entire annular gap, with the higher-concentration region located near the outer cylinder wall and still predominantly in the lower half due to the persistent influence of gravity. The streamwise particle velocity field tends toward axisymmetry, yet distinct left-right asymmetries are observed, arising from the combined effect of rotation and gravity. The particle streamlines in the (r-θ) plane are nearly axisymmetric; however, particles traveling close to the inner wall collide with it in the upper half of the annulus, where insufficient momentum prevents them from overcoming gravity. In Regime 3 (rotation-dominant), centrifugal effects dominate particle transport in the case of strong rotational forcing. Particles distribute axisymmetrically along the outer cylinder wall, a pattern mirrored in the streamwise particle velocity, which becomes uniformly distributed in both magnitude and spatial extent across the outer wall or annular gap. The particle streamlines adopt concentric circular trajectories, indicating that the dynamic are governed primarily by rotation, with particles following the rotational paths of the carried fluid.
Diskussion
In this study, the flow regimes within horizontal particle-laden annular configurations with inner wall rotation are classified using the present multiphase model. A systematic parametric investigation is conducted to examine the effects of N, St, Fr and Φₘ on the flow behavior. Three distinct flow regimes have been identified. These regimes are characterized based on the particle concentration, particle streamwise velocity and the particle streamlines, under conditions of near-elastic collisions for both particle-wall and inter-particle interactions: Regime 1 (gravity-dominant), Regime 2 (gravity-rotation-competitive) and Regime 3 (rotation-dominant). The interplay of these parameter combinations is thereby analyzed within these specific concentric annular configurations.
