Scalable Task-Driven Robotic Swarm Control via Collision Avoidance and Learning Mean-Field Control
Kai Cui_Scalable Task-Driven Robotic Swarm Control via Collision Avoidance and Learning Mean-Field Control_Figure1Figure 1: A hierarchical overview of our approach. The learned high-level mean-field control policy sends movement instructions to the (UAV) swarm, while each agent uses a real-time collision avoidance algorithm – here artificial potential fields (APF) – to avoid collisions with others.
Kai CuiEinleitung
In recent years, reinforcement learning and its multi-agent analogue have achieved great success in solving various complex control problems. However, multi-agent reinforcement learning remains challenging both in its theoretical analysis and empirical design of algorithms, especially for large swarms of embodied robotic agents where a definitive toolchain remains part of active research. We use emerging state-of-the-art mean-field control techniques in order to convert many-agent swarm control into more classical single-agent control of distributions. This allows profiting from advances in single-agent reinforcement learning at the cost of assuming weak interaction between agents. However, the mean-field model is violated by the nature of real systems with embodied, physically colliding agents. Thus, we combine collision avoidance and learning of meanfield control into a unified framework for tractably designing intelligent robotic swarm behavior. On the theoretical side, we provide novel approximation guarantees for general mean-field control both in continuous spaces and with collision avoidance. On the practical side, we show that our approach outperforms multi-agent reinforcement learning and allows for decentralized open-loop application while avoiding collisions, both in simulation and real UAV swarms. Overall, we propose a framework for the design of swarm behavior that is both mathematically well-founded and practically useful, enabling the solution of otherwise intractable swarm problems. Our contribution can be summarized as follows: (i) We combine reinforcement learning (RL) with mean field control (MFC) and collision avoidance algorithms for general taskdriven control of robotic swarms; (ii) We give novel theoretical approximation guarantees of MFC in finite swarms as well as in the presence of additional collision avoidance maneuvers; (iii) We demonstrate in a variety of tasks that MFC outperforms state-ofthe-art MARL, can be applied in a decentralized open-loop manner and avoids collisions, both in simulation and real UAV swarms. Overall, we provide a general framework for tractable swarm control that could be applied directly to swarms of UAVs.
Methoden
In order to tractably describe a plethora of swarm tasks, we formulate a mean-field model where all agents are anonymous and it is sufficient to consider their distribution. Since MARL can be difficult in the presence of many agents (combinatorial nature), we will formulate and verify a limiting infinite-agent system, starting from a finite-agent swarm system. In the limit as N → ∞, single agents become indiscernible and we need only model their distribution (mean-field).
Ergebnisse
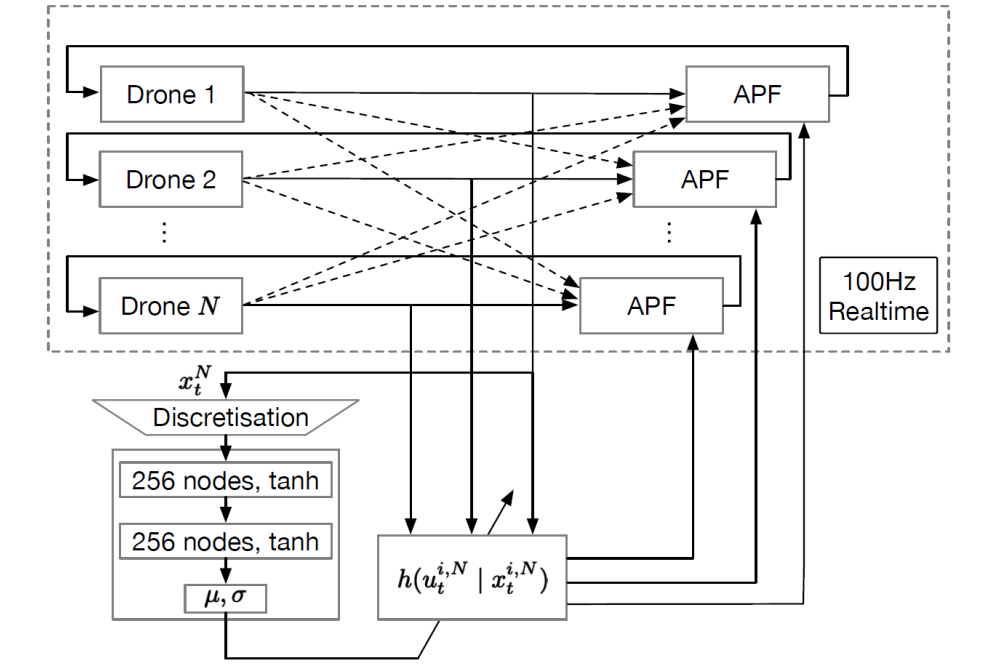
As long as continuity conditions are fulfilled, i.e. small changes in the agent distribution lead to small changes in reward, the MFC model is a good approximation for large swarms and its solution solves the finite agent system approximately optimally. As existing approximation properties still remain limited to finite state and action spaces, we give a brief, novel proof for compact spaces. As a result, the MFC approach is a theoretically rigorous approach to approximately optimally solving large-scale swarm problems with complexity independent of N. In order to remove the two remaining obstacles of (i) solving the MFC problem, and (ii) resolving the real-world gap of MFC for embodied agents, we combine MFC with arbitrary powerful RL and collision avoidance techniques. The overall hierarchical structure is found in Fig. 1. The MFC solution is learned via RL and gives high-level directions, which are realized by each agent while avoiding collisions. A solution of the mean-field system does not directly translate into applicable real-world behavior, since the mean-field solution ignores physical constraints. While e.g. UAVs could fly at different heights, a general swarm algorithm should explicitly avoid collisions in order to guarantee suitability of the weakly interacting MFC model. This is done by separating concerns, decomposing the issue into MFC plus sequences of collision avoiding navigation subproblems between decision epochs. For example, we could choose U slightly smaller than the maximum speed range to allow for additional avoidance maneuvers. Then, assuming the time Δt between two MFC decisions t and t + 1 is sufficiently long, and that agents have finer, direct control over their positions, a collision-avoiding navigation subroutine could approximately achieve the desired positions up to an error that becomes arbitrarily small with agent radius r. We can then show that a collision-avoiding finite swarm of sufficiently many small agents is solved well by our approach. We consider three problems of increasing complexity to demonstrate our approach. We successfully show results demonstrating the power of our MFC framework for task-driven swarm control, namely their theoretical and numerical advantage over standard MARL, the potential for decentralized open-loop control, and the influence of collision avoidance on optimality, both in simulation and in the real world.
Diskussion
In this work, we have proposed a scalable task-driven approach to robotic swarm control that allows for model-free solution of swarm tasks while remaining applicable in practice by using deep RL, MFC and collision avoidance. Our approach is hierarchical, in principle allowing to profit from any state-of-the-art RL and collision avoidance techniques. Our work is a step towards general toolchains for robotic swarm control, which yet remain part of active research. We have solved part of the limitations of mean-field theory for embodied agents by integrating collision avoidance into the toolchain, but more work on more sparsely interacting mean field models may be necessary, e.g. for UAV-based communication with strongly neighbor-dependent interaction, by incorporating graph structure. Extensions to non-linear dynamics and dynamical constraints may be fruitful. Lastly, while our Gaussian parametrization of P(U) is efficient, the state discretization still suffers from a curse of dimensionality, as the number of bins rises quickly with fineness of discretization, which is state of the art and could be supplemented e.g. by visual techniques.
