Electronic Pairing in Low-Dimensional Systems from Lattice Density-Functional Theory
Electronic Pairing 1Fig. 1: Pairing energy ΔEp of the attractive Hubbard model as a function of the number of electrons Ne in one-dimensional rings.
Electronic Pairing 2Fig. 2: Pairing energy ΔEp of the attractive Hubbard model on a Bethe lattice as a function of 1/(z − 1), where z is the local coordination number (see inset).
Einleitung
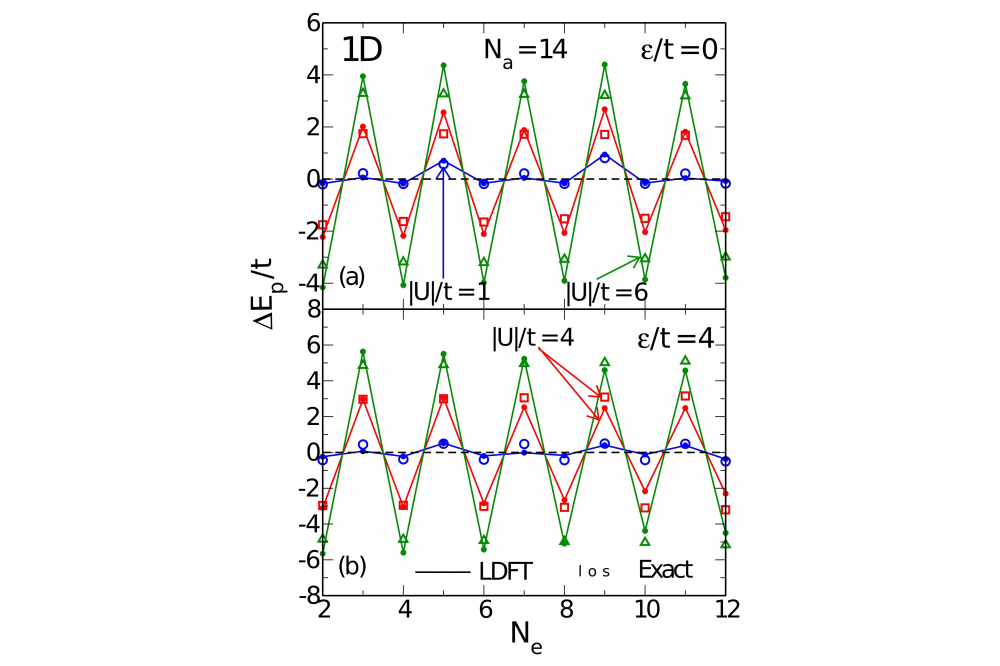
The properties of strongly interacting electrons subject to local pairing interactions have been investigated theoretically in the framework of lattice density functional theory (LDFT). The ground-state properties and pairing interactions have been calculated by using the single-particle density matrix as basic variable of the many-body problem. Remarkable even-odd and supereven oscillations of the pairing energy ΔEp have been observed as a function of band filling. Comparison with exact numerical Lanczos diagonalizations and densitymatrix renormalization-group calculations show that LDFT yields a very good quantitative description of the properties of the model in the complete parameter range, thus providing a significant improvement over mean-field approaches. The role of dimensionality on the pairing coupling ΔEp has been revealed.
Methoden
The study of strong electron-correlation phenomena and in particular the description of pairing mechanisms leading to superconductivity remain a major challenge in condensed-matter physics. In conventional superconductors, pairing of electrons is known to be induced at the Fermi energy by an effective off-diagonal attractive interaction mediated by phonons. An alternative approach to study the consequences of electronic pairing in metals is to consider the Hubbard model with attractive local interactions. In contrast to the BCS Hamiltonian, the Hubbard interaction is strictly local in real space. It involves pairs of electrons occupying the same lattice site with opposite spins. It is therefore considerably important to investigate the properties resulting from such contrasting types of interactions.
Ergebnisse
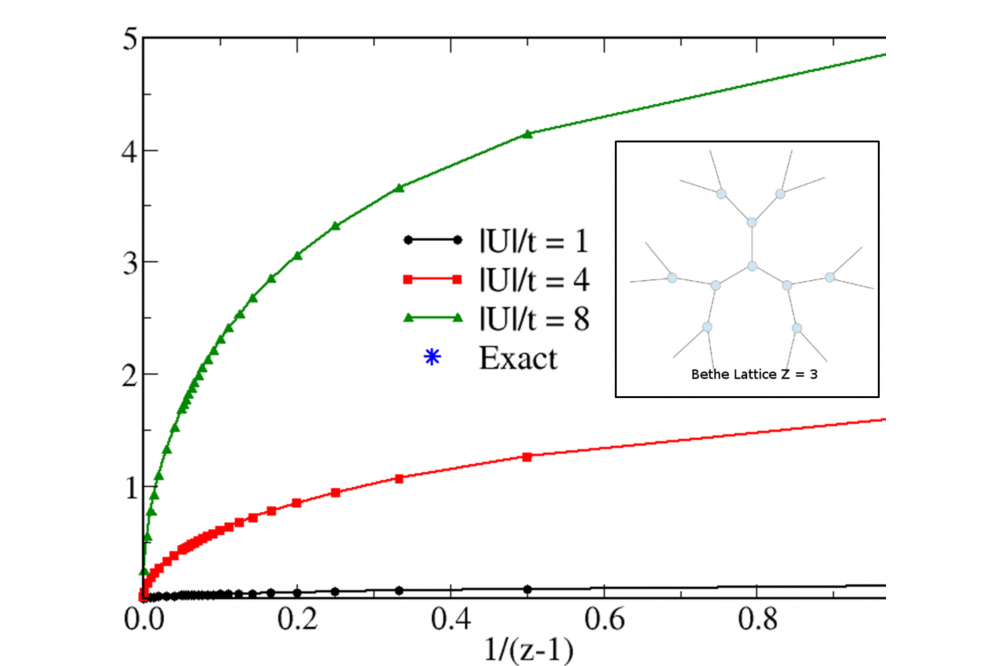
In this work the attractive Hubbard model has been studied in the framework of lattice-density functional theory. The ground-state energy E = T + W is regarded as a functional of the single-particle density matrix γij with respect to the lattice sites, where T[γ] represents the kinetic and crystal-field energies and W[γ] the interaction energy. Aside from the exactly known kinetic energy functional T[γ], we have proposed a simple scaling approximation to the attractive interaction energy W[γ], which is based on exact analytic results for the Hubbard dimer and on a scaling hypothesis within the domain of representability of γ. A computer program has been developed from which the groundstate properties are derived. For the applications of the theory we consider one-, two-, and three-dimensional finite and extended bipartite lattices having homogeneous or alternating onsite energy levels. In addition, the Bethe lattice is investigated as a function of coordination number. The kinetic, Coulomb, and total energies, the density distribution γii, nearest-neighbor bond order γij , and pairing energy ΔEp have been determined as a function of the interaction strength |U|/t, onsite potential ε/t, and band filling n = Ne/Na.
