Sparse Mean Field Control for Multi-Agent Systems
Christian Fabian_Learning Mean Field Games on Sparse Graphs_Figure1Figure 1: Four networks, each with around 15k nodes and 50k edges. The Erdös-Renyi graph (left) generated by a standard graphon does not have any high degree nodes. The Lp graphon graph (middle left) has a few high degree nodes expressed by the flat degree distribution tail. The graphex (middle right) and real subsampled Flickr network (right) show a very similar degree distribution with rather broad tails and a core-periphery like structure.
Christian Fabian
Christian,Fabian_ Sparse Mean Field Control for Multi-Agent Systems_Fig2Figure 2: Comparison of the empirically observed MF (real) with the predicted MF fordifferent problems and real world networks for four different mean field models. LW and LW* denote two versions of our new LWMFC approach while GX and LP are existing approaches named GXMFGs and LPGMFGs which are based on graphexes and Lp graphons, respectively.
Einleitung
Large agent networks are abundant in applications and nature and pose difficult challenges in the field of multi-agent reinforcement learning (MARL) due to their computational and theoretical complexity. While graphon mean field games and their extensions provide efficient learning algorithms for dense and moderately sparse agent networks, the case of realistic sparser graphs remains largely unsolved. Thus, we propose a novel mean field control model inspired by local weak convergence to include sparse graphs such as power law networks with coefficients above two. Besides a theoretical analysis, we design scalable learning algorithms which apply to the challenging class of graph sequences with finite first moment. We compare our model and algorithms for various examples on synthetic and real world networks with mean field algorithms based on Lp graphons and graphexes. As it turns out, our approach outperforms existing methods in many examples and on various networks due to the special design aiming at an important, but so far hard to solve class of MARL problems. Leveraging local weak convergence, we formulate our new local weak mean field control (LWMFC) model. LWMFC provides a theoretically motivated framework for learning agent behavior in challenging large empirical networks where the average expected degree is finite, but the degree variance may diverge to infinity. On the algorithmic side, we provide a two systems approximation for LWMFC and corresponding learning algorithms to approximately learn optimal behavior in these complex agent networks. Finally, we evaluate our novel LWMFC learning approach for multiple problems on synthetic and real-world networks and compare it to different existing methods mentioned above. Overall, our contributions can be summarized as follows: we introduce LWMFC to model large cooperative agent populations on very sparse graphs with finite expected average degree, give a rigorous theoretical analysis and motivation for LWMFC, provide a two-systems approximation and scalable learning algorithms for LWMFC, and show the capabilities of our LWMFC learning approach on synthetic and real world networks for different exemplary problems.
Methoden
Our approach leverages the local weak convergence principle from graph theory which enables a theoretically well-founded depiction of sparse graph topologies. By employing local weak convergence, we are able to extend the mean field control setup to very sparse graphs. To ensure that the runtime of our developed learning algorithms remains manageable for arbitrary sizes of agent networks, we furthermore develop a two systems approximation. In this two systems approximation, highly connected individuals and agents with only few connections are considered as parts of different subsystems to facilitate our scalable learning algorithms.
Ergebnisse
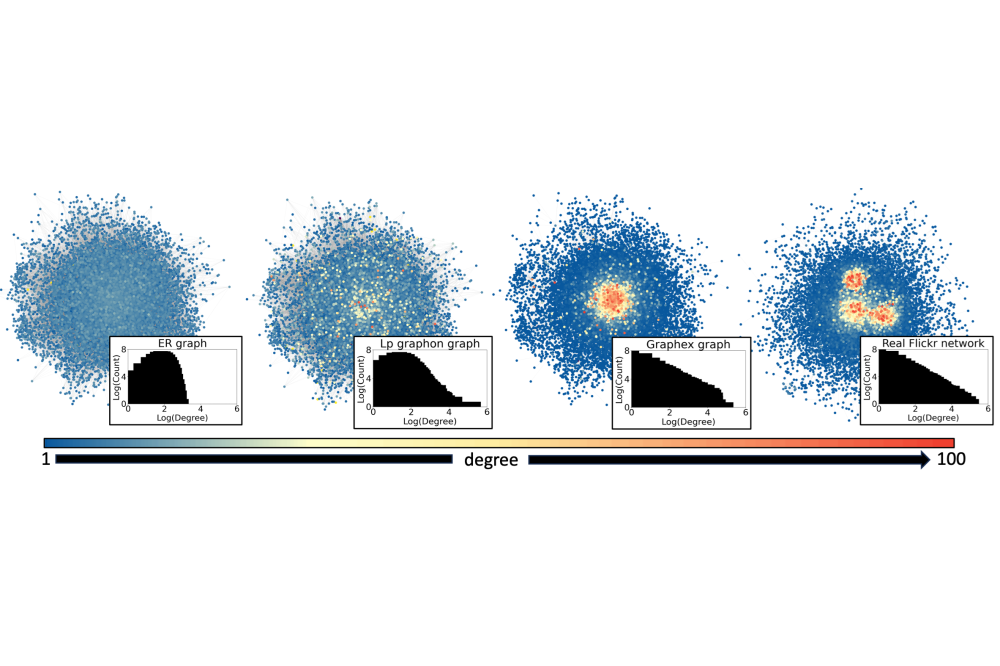
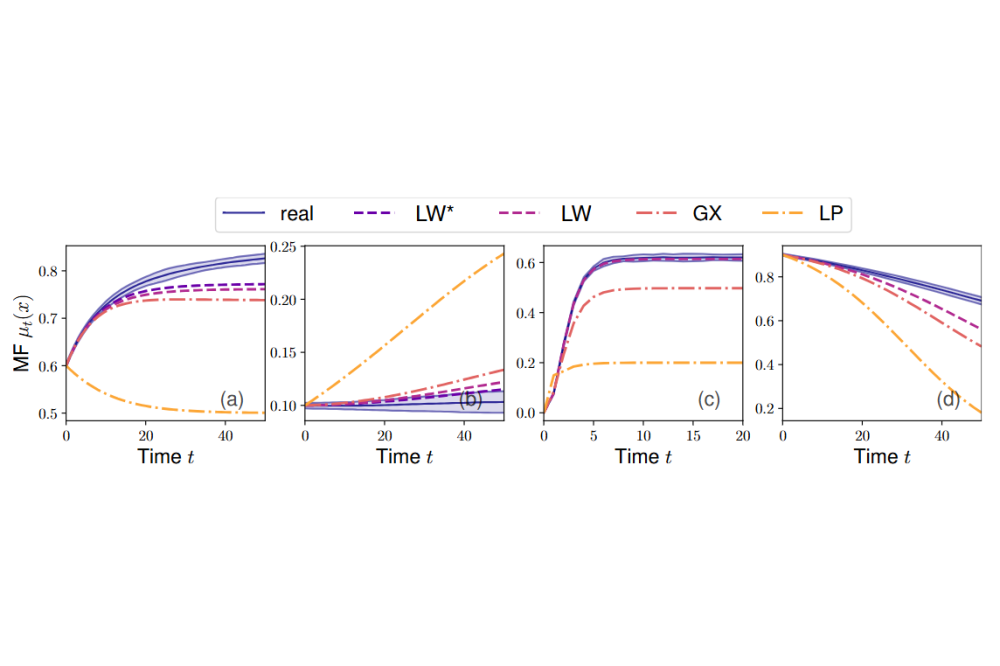
The empirical evaluation conducted in our work indicates that our proposed LWMFC approach outperforms existing approaches like LPGMFGs and GXMFGs on graphs which exhibit a considerable degree of sparsity, see Figure 2 for exemplary visualizations. In contrast to these existing approaches, LWMFC is designed for graph sequences where the average degree does not converge to infinity as the number of agents goes to infinity. Although the LWMFC approach outperforms the methods from the literature in our examples, LWMFC and the corresponding two systems approximation still do not capture the empirical mean field evolution perfectly. Thus, a promising direction for future work could be to further refine the two systems approximation.
Diskussion
We have introduced the novel LWMFC framework which can depict agent networks with finite expected degree and diverging variance. After a theoretical analysis, we provided a practical two systems approximation which was then leveraged to design scalable learning algorithms. Finally, we evaluated the performance of our model and learning algorithms for different problems on synthetic and real-world datasets and compared them to existing methods. For future work, one could extend the LWMFC model to various types of specific mean field models, e.g. to partial observability or agents under bounded rationality. We hope that LWMFC and the corresponding learning approaches prove to be a versatile and useful tool for researchers across various applied research areas.
