Three-Dimensional Core-Collapse Supernova Simulations With Nuclear Reaction Networks
Navo_Gerard_Three-Dimensional Core-Collapse Supernova Simulations With Nuclear Reaction Networks_Fig1Figure 1: Top left panel shows the maximum (dashed), average (solid), and minimum (dotted) position of the shock. Top right panel displays the ratio of advection over heating timescales in the gain layer. Middle panels show the diagnostic (left) and turbulent (right) energy.
Dr. Gerard NavóEinleitung
Massive stars end their life in core-collapse supernovae (CCSN). These explosive events are triggered by the collapse of the iron core and release into the interstellar medium several solar masses of products that were synthesized during the stellar evolution and the explosion itself. In order to investigate the mechanisms involved, radiation-hydrodynamic simulations are performed, e.g., [1], following different evolutionary stages from collapse to shock breakout. Nevertheless, the whole puzzle is still far from being completed and state-of-the-art CCSN simulations still have much room for improvement. In this work, we focus on the impact of the different ways to treat nuclear reactions and the associated energy generation in the simulations [2].
A nuclear reaction network evolves the abundances of nuclei by solving a system of ordinary differential equations including all the reactions between the species. In CCSNe, it can include some several hundred nuclei and, thus, including them in multidimensional CCSN simulations is very challenging. Therefore, simulations usually employ an approximated treatment of the composition, e.g. [3], and a detailed nucleosynthesis is then obtained by postprocessing [4].
In this project, we aim to obtain three-dimensional models with different networks to study their impact on the dynamics of the explosion and the nucleosynthesis. We introduced two different models:
- One model employing a very reduced network, a 16 alpha-chain (RN16), responsible for most of the nuclear energy released in the explosion (3DRN16).
- A second model employing a large in situ network, that evolves 94 species and mimics a larger one of 242 (RN94). This will allow us to follow the nucleosynthesis in the simulation with an unprecedented accuracy. However, this model is more computationally expensive.
Methoden
In [2], we implemented a reduced network module in the simulations code Aenus-Alcar [5], and observed that they have a noticeable impact on the dynamics of the explosion and the nucleosynthesis.
We perform our simulations with the Aenus-Alcar code [5, 6]. It combines special relativistic hydrodynamics (HD), a pseudo-relativistic gravitational potential, and state-of-the-art two-moment (M1) neutrino transport. The HD equations consist on a hyperbolic system of PDEs that is discretized into a spatial grid by using an upwind constrained-transport scheme. The treatment of gravity goes beyond the classical description by including correction terms to the Newtonian gravitational potential according to [7]. In spherical coordinates, which we will use here, the corresponding elliptic equations are solved using a solver based on a multipole expansion [8]. The two-moment neutrino transport [e.g., 9] reduces the complexity of the Boltzmann equation to only two equations which correspond to the first two angular moments, i.e. the neutrino energy and flux, and are closed by an algebraic Eddington factor. The system is discretized into several energy bins that encompass the possible neutrino energies and flavors, and is coupled to the HD equations.
The reduced network module ReNet [2] is coupled by a source term to the HD equations and allows to calculate abundance flows for networks of different sizes and complexities. It solves the set of ordinary first-order differential equations in an implicit way. The integration scheme is a first-order implicit Euler scheme [10]. The convergence criterion of the necessary Newton-Raphson scheme is given by, e.g., the mass conservation. We consequently use solvers for dense matrices. We furthermore assume some species to be in steady state in order to consider them indirectly and to avoid using an extra differential equation for them, which allows to save computational cost.
Within this project, we have successfully computed t = 1.5 s and t = 0.845 s of evolution of the proposed models 3DRN16 and 3DRN94, respectively.
Ergebnisse
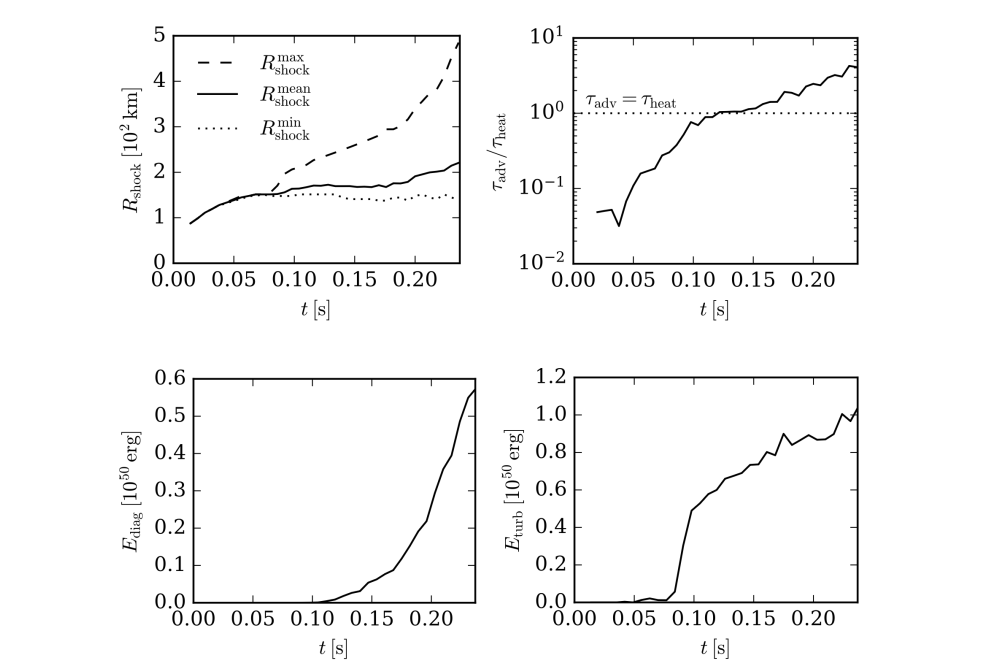
As mentioned above, the 3DRN16 simulation has already achieved 1.5 s, which we think is the minimum time this model needs for its ejecta to cool down and be able to compute its nucleosynthesis. Therefore, this simulation has already finished. The only published material to date (Navó 2024) focused at the first 241 ms post-bounce (460 ms of evolution) (see Figure 1).
Diskussion
As shown in Figure 1, the ratio τadv/τheat exceeds unity shortly after t = 100 ms post-bounce. This indicates that the heating timescale is shorter than the advection timescale, neutrinos deposit energy faster than what the fluid takes to accrete to the proto-neutron star (PNS), and, therefore, the explosion is likely to trigger. This is enhanced by the growth of turbulence in the post-shock layer, which leads to non-radial motions of the matter, and hence, it is longer times exposed under a strong neutrino heating. In addition, turbulent motion adds an extra pressure that drives the shock further outwards. From this moment, the diagnostic explosion energy Ediag begins to rise, and the maximum shock radius expands linearly. By t=460 ms of simulation, both Ediag and Rmaxshock, which is the maximum shock radius, are increasing rapidly. The former reaches a value of approximately Ediag ≃0.55 ×1050 ,erg, which corresponds to about 25−50% of the typical explosion energies found in 3D models in the literature. The maximum shock radius is significantly developed, reaching Rmaxshock ≃500,km. The difference between Rmaxshock and Rminshock hints at how far the explosion is from spherical symmetry. The evolution of these metrics at these early times already indicated that 3DRN16 was likely to undergo an energetic explosion, as it finally did. Additionally, the continued growth of Ediag and the further expansion of the shock radius supported the prospect of explosion.
