GPU-Accelerated Solution of Many Small ODE Systems for High-Temperature Component Lifetime Modeling
Durst_Tobias_GPU-Accelerated Solution of Many Small ODE Systems for High-Temperature Component Lifetime Modeling_Fig1Figure 1: Performance comparison of SUNDIALS, Euler, CPU and GPU architectures.
Tobias Durst
Durst_Tobias_GPU-Accelerated Solution of Many Small ODE Systems for High-Temperature Compo- nent Lifetime Modeling_Fig2Figure 2: Relative Speedup of Different Solver Implementations.
Tobias Durst
Durst_Tobias_GPU-Accelerated Solution of Many Small ODE Systems for High-Temperature Compo- nent Lifetime Modeling_Fig3Table 1: Effects of floating-point precision with varying datatypes for Input, Math (e.g. ∆D computation), and Storage (e.g. D, with D being the Damage ODE variables). ∆Mean indicates the percentage difference relative to the all-64-bit configuration.
Tobias DurstEinleitung
Predicting the lifetime of components designed for very high temperatures is crucial for improving the efficiency and reliability of many technologies, such as power plants and aircraft engines. However, accurately estimating how long these components will last under extreme heat is incredibly challenging from a computational perspective. These predictions often rely on solving complex sets of mathematical equations known as Ordinary Differential Equations, or ODEs. One such advanced model is the Chaboche model, which is known for its accuracy in describing material behavior at high temperatures.
To make lifetime predictions for a component, engineers often need to analyze it as a three-dimensional structure, which is broken down into a mesh of many small points, sometimes up to 100,000. For each of these points, the complex ODEs, like the Chaboche model, must be solved. Furthermore, to account for uncertainties in material properties and operating conditions, a statistical approach is often used. This means repeating the entire calculation thousands of times with slightly different input parameters. Combining these factors results in a massive computational task. Using traditional computers to solve these problems can take months, making it impractical for timely engineering decisions.
Methoden
In this project, we investigated the use of Graphics Processing Units (GPUs) to significantly speed up the process of solving the Chaboche model equations. GPUs are specialized processors that excel at performing many calculations simultaneously, making them well-suited for computationally intensive tasks. We began by testing a sophisticated software library called SUNDIALS, specifically designed for solving ODEs, in combination with GPU acceleration. We used a special version of SUNDIALS that is designed to work efficiently with GPUs and wrote custom code (kernels) that run on the GPU to perform the core calculations of the Chaboche model.
Next, we explored simpler numerical methods, such as the Forward Euler method, to solve the ODEs. We created specialized GPU kernels tailored for this simpler method to maximize performance and evaluated the effects of different data types and sizes. Finally, we tested a simplified, or ”reduced,” version of the Chaboche model to see if it could further improve computational efficiency without sacrificing accuracy.
Ergebnisse
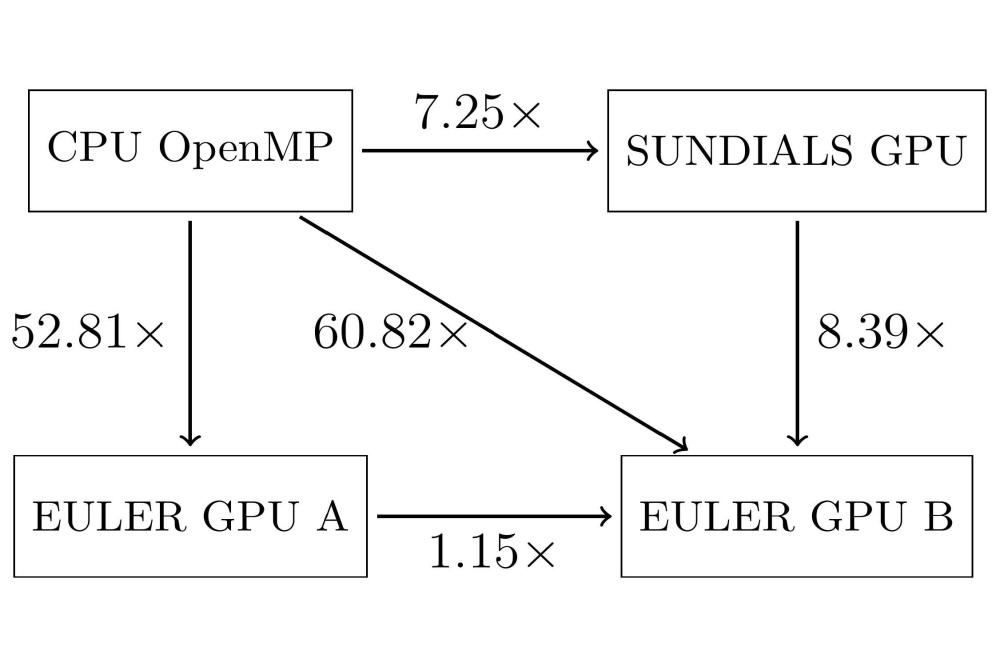
Our tests showed that using GPUs provided a substantial performance boost. When using SUNDIALS with GPU acceleration, we achieved a speedup of approximately 7.25 times compared to using a traditional computer processor. However, even greater speedups were achieved with the simpler Forward Euler method, reaching 40 to 60 times faster performance depending on the specific test conditions.
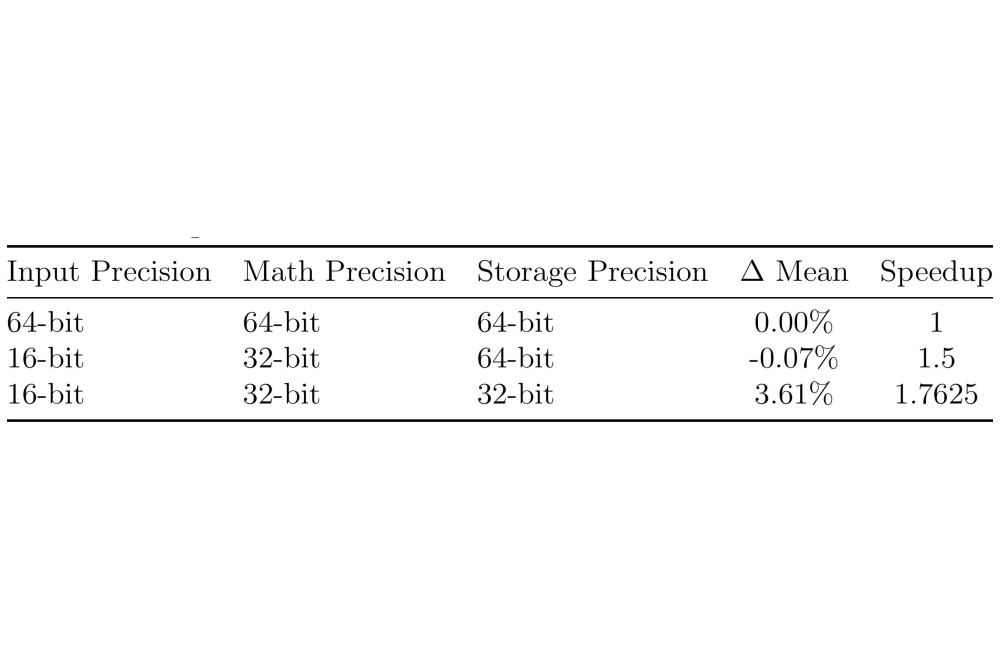
We also found that carefully choosing the data types used in the calculations could further improve performance. Using ”half” precision (16 bit) for the input data, instead of the more common ”double” precision (64 bit), resulted in a speedup of around 1.5 times with almost no noticeable loss in accuracy. Using ”single” precision (32 bit) for the main mathematical calculations offered an even greater speedup of about 1.76 times, but at the cost of a small accuracy loss of approximately 3.6%.
The reduced version of the Chaboche model shifted the computational bottleneck from the calculations themselves to the speed at which data could be accessed from memory. This resulted in a modest performance increase of about 15% with negligible impact on accuracy. Ultimately, by combining GPU acceleration, optimized numerical methods, and data type choices, our final solver was capable of solving one billion equations in approximately 20 hours using a single high-performance GPU (V100). By using 8 GPUs together, we were able to reduce this computation time to just 2 hours and 25 minutes.
Diskussion
Our findings clearly demonstrate the significant performance gains achievable by switching from traditional CPUs to GPUs for solving complex lifetime prediction problems. We observed dramatic speed improvements, allowing us to tackle problems that were previously computationally infeasible. Furthermore, we showed that additional performance improvements can be gained by carefully optimizing the numerical methods used, choosing appropriate data types, and even simplifying the underlying physical models.
These results highlight the immense potential of GPU-accelerated High Performance Computing for enabling more accurate and efficient lifetime predictions for high-temperature components, which can lead to improved designs, optimized maintenance schedules, and ultimately, more reliable and efficient energy and engineering systems.
