Beyond Ni-Based Superalloys
Beyond Ni-based SuperalloysFigure 1: Atomic structure of Zr alloyed tilt Σ5(310)[001] GB in molybdenum. For distinguishing between Mo atoms that belong to different grains, red and yellow spheres are used. Green sphere represents Zr atom.
Olena LenchukEinleitung
Improving the efficiency, performance and cost-effectiveness of energy production will depend critically on our capability to develop substantially improved materials and material systems as well as on our ability to understand and to design their properties. Turbine blades, for example, working inside the hottest part of the gas turbine are exposed to significant environmental and mechanical stresses and thus need to be resistant to creep, fatigue and oxidation. Nickel-based superalloys are traditionally used to sustain the most stressed parts of turbine blades, but have a limited service temperature (around 1000 °C) [1, 2]. Applying materials with higher melting points in turbines would allow to operate these components with increased gas inlet temperatures and to optimize the thermodynamic behaviour leading to a reduction of fuel consumption, emissions and costs. Molybdenum-based alloys are good candidate materials for such high-temperature applications due to their high strength and creep resistance at elevated temperatures with high thermal conductivity and a low coefficient of thermal expansion [3, 4]. However, to meet the requirements for the desired applications, fracture toughness and ductility at ambient temperatures need to be improved [5-7]. The former finding is predominantly due to grain boundary embrittlement by oxygen and nitrogen [5, 8]. One common approach for improving ductility is microalloying with suitable elements that may suppress oxygen and nitrogen segregation at the grain boundaries. Experimental studies show that microalloying with Zr is an efficient way to improve the ductility and to increase the fracture toughness of both, Mo and Mo-based alloys [9, 10, 11]. However, the physical origin of this effect is not clear. At this point, total-energy calculations based on the density-functional theory (DFT) are useful for obtaining a detailed understanding of the energetics on the atomic scale.
Methoden
Total-energy calculations are performed using the projector-augmented planewave code vasp [12, 13] in conjunction with the GGA-PBE [14] exchange-correlation functional. Blöchl’s projector augmented wave (PAW) method [15] is used to define pseudopotentials. The tilt Σ5(310)[001] grain boundary (GB) is represented in a periodic supercell of 160 atoms and consists of two equivalent GBs. The calculations are done using a planewave energy-cutoff of 450 eV, and the Brillouin zone is sampled with a grid of 2x6x8 generated by Monkhorst-Pack method [16]. The structural optimization is performed via the conjugate-gradient method by full relaxation of the internal coordinates of atoms, until the residual forces on individual atoms are converged to less than 0.01 eV/Å2.
Ergebnisse
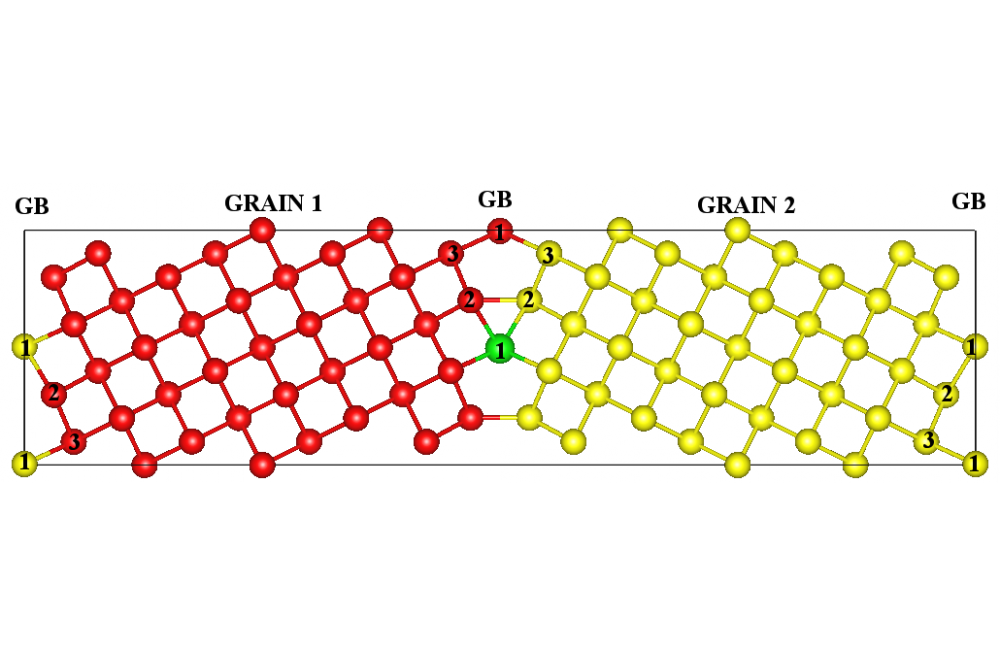
Figure 1 illustrates the structural models of the tilt Σ5(310)[001] model grain boundary (GB). This high-angle GB is constructed by tilting the bcc Mo cell by an angle of 36.9° around the [001] axis. Non-equivalent lattice sites within the GB are marked by “2” and “3”, whereas coincidence sites are marked as “1”. We replace one Mo atom by Zr on each non-equivalent lattice site within the grain boundary and optimize the structure. By comparing the formation energy of Zr in the GB relative to Zr in the bulk, we determine a thermodynamical driving force for segregation. The formation energy is defined as:
Ef = E(GB + yZr) - E(GB) - y·ε(Mo2Zr) + (1 + 2y)·ε(Mo).
Here, E(GB + yZr) and E(GB) are the total energies of the defective (containing a substitutional Zr atom) and pure GB model, respectively. The total energy of bulk molybdenum per
Mo atom is represented by ε(Mo). Mo2Zr is used as a reference state for Zr, since the pure Mo phase is in equilibrium with the Mo2Zr phase if the Zr content is increased [17]. Changes in the formation energy of Zr occupying non-equivalent lattice sites within the grain boundary relative to a position in the bulk Mo (Ef(bulk Mo) = 0.27 eV) are -0.51 eV for the position “1”, -0.17 eV for the position “2” and -0.15 eV for the position “3”. The negative values correspond to the reduction in energy which reveals the existence of a strong driving force for GB segregation. Zr being an oversized alloying additive relative to Mo atom prefers to occupy sites with a sufficient free volume, which is a site “1” (see Figure 1).
Ausblick
In this report we have presented calculations of Zr segregation at the grain boundary in molybdenum based on density-functional theory (DFT) calculations. Our results reveal the driving force of Zr to segregate to Mo grain boundary. As the next step, the effect of Zr on the GB cohesive strength has to be investigated. To obtain results independent of the GB orientation, another GB configuration should be constructed.
