Metric Self-Paced Reinforcement Learning
Klink, Pascal_Metric Self-Paced Reinforcement LearningFigure 1: An example of the bipedal walker environment, in which we parameterize the size
(x-axis) as well as the spacing (y-axis) of obstacles. The colored dots represent tasks that
have been generated by our method. Dark colors indicate tasks that have been trained on in early
stages, and bright colors show tasks that have been generated towards the end of training. We
see that the our method increases the obstacle size as training progresses, simultaneously
adapting the maximum size based on the spacing between the obstacles.
Einleitung
Reinforcement Learning (RL) is a promising tool for solving complicated control and decision-making tasks in a data-driven manner. However, current methods typically require some form of regularization in order to deliver acceptable solutions for complicated tasks. Many of these regularizations, such as reward design, are not very well understood from a theoretical perspective.
Curriculum reinforcement learning aims to formalize one particular form of regularization: Training the RL agent on a tailored sequence of learning tasks. Such well-chosen task sequences can allow using simple binary reward functions instead of hand-crafted ones, avoiding the pitfalls of misspecified reward functions.
In this project, we investigate ways to automatically generate an appropriate curriculum that improves the learning performance of an agent by exploiting notions from optimal transport.
Given the compute-intensive evaluations over parameter settings as well as test environments, the Lichtenberg cluster was an ideal choice to accelerate the development cycle of our project.
Methoden
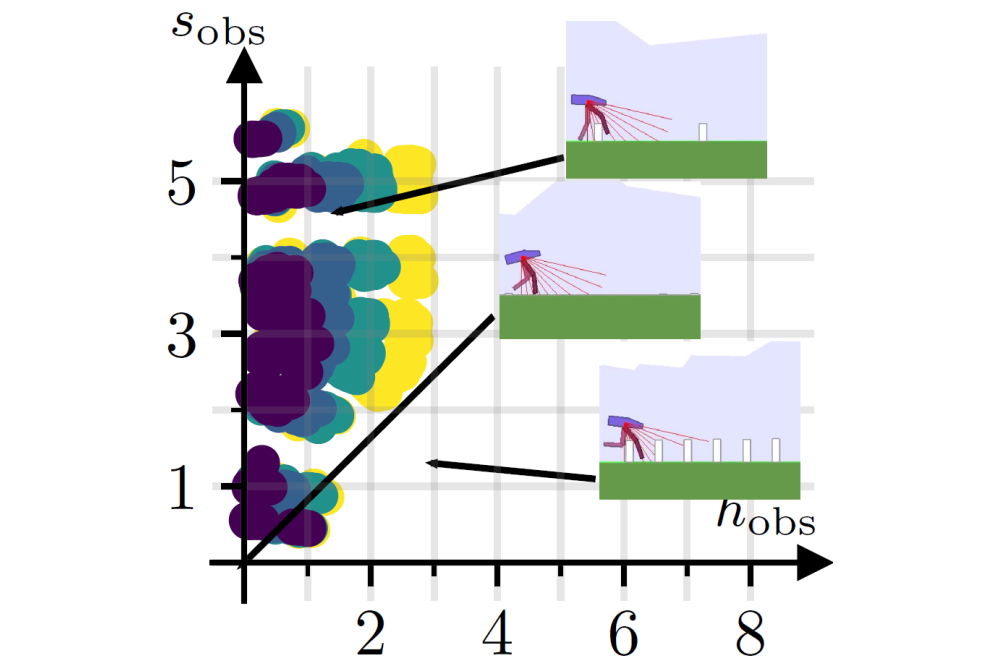
We formalized the curriculum generation as an optimal transport problem which aims to morph a distribution of easy training tasks into a distribution of (challenging) target tasks. The benefit of this formulation is the incorporation of a distance function which allows the RL practitioner to specify the similarity between learning tasks. The optimal transport interpolations are then resulting in a gradual change in the learning tasks according to the specified distance function, allowing the agent to learn in increasingly challenging tasks. This interpolation process is additionally constrained to avoid generating tasks that are too complex for the reinforcement learning agent given its current capabilities.
We evaluated our method on two environments that test the avoidance of suboptimal behavior and require dealing with sparse rewards respectively. Furthermore, we evaluated our method on a simulated bipedal walker task, in which the walker was required to overcome increasingly complicated obstacle parkours.
Ergebnisse
The evaluation showed that our method allowed the reinforcement learning agent to learn the desired behavior where default learning was not possible. Furthermore, our method performed either as well as or better as alternative curriculum reinforcement learning methods and our previous work.
Diskussion
Given the positive outcomes of these first evaluations, we aim to improve the method in the future, e.g. by allowing its application to non-Euclidean task parameterizations or simply improving speed and robustness. Both extensions will allow the approach to be more widely applied, hopefully enabling future downstream improvements.
Additionally, we aim to showcase the benefit of our method in a real-world reinforcement learning scenario, e.g. in robotic control tasks of underactuated systems, in which the complexity of the control tasks is gradually increased e.g. by amplifying encountered disturbance forces or the complexity of the trajectory to be generated.
